
Nhà máy đường kiểm tra khối lượng các gói đường do một máy đóng gói tự động thực hiện. Kết quả kiểm tra được biểu diễn trong bảng dưới đây:
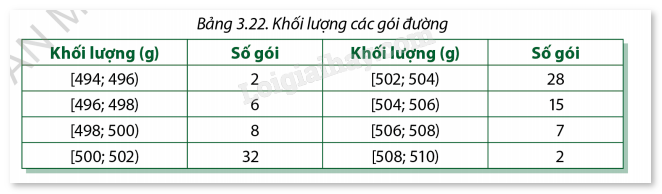
a) Tính trung bình và độ lệch chuẩn của khối lượng các gói đường.
b) Có thể nói là máy vận hành tốt hay không nếu như tiêu chuẩn mong muốn của nhà máy là khối lượng trung bình nằm trong khoảng 500 – 504 gam và độ lệch chuẩn nhỏ hơn 3 gam?

- Công thức tính trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)

a) Tính trung điểm của từng lớp khối lượng.
Advertisements (Quảng cáo)

Tính trung binh \(\overline x \).
\(\bar x = \frac{{2 \cdot 495 + 6 \cdot 497 + 8 \cdot 499 + 32 \cdot 501 + 28 \cdot 503 + 15 \cdot 505 + 7 \cdot 507 + 2 \cdot 509}}{{2 + 6 + 8 + 32 + 28 + 15 + 7 + 2}}\)
\(\bar x = \frac{{990 + 2982 + 3992 + 16032 + 14084 + 7575 + 3549 + 1018}}{{100}} = \frac{{50222}}{{100}} = 502,22\;{\rm{g}}\)
Tính \(\sum {{f_i}x_i^2} \)
\(\sum {{f_i}} x_i^2 = 2 \cdot {(495)^2} + 6 \cdot {(497)^2} + 8 \cdot {(499)^2} + 32 \cdot {(501)^2} + 28 \cdot {(503)^2} + 15 \cdot {(505)^2} + 7 \cdot {(507)^2} + 2 \cdot {(509)^2}\)
\(\sum {{f_i}} x_i^2 = 2 \cdot 245025 + 6 \cdot 247009 + 8 \cdot 249001 + 32 \cdot 251001 + 28 \cdot 253009 + 15 \cdot 255025 + 7 \cdot 257049 + 2 \cdot 259081\)
\(\sum {{f_i}} x_i^2 = 490050 + 1482054 + 1992008 + 8032032 + 7084252 + 3825375 + 1799343 + 518162 = 25223276\)
Độ lệch chuẩn của khối lượng các gói đường là:
\(S = \sqrt {\frac{{25223276}}{{100}} - {{\left( {502,22} \right)}^2}} \approx 2,798g\)
b) Khối lượng trung bình \(\overline x = 502,22\) nằm trong khoảng yêu cầu [500,504]. Độ lệch tiêu chuẩn \(S \approx 2,798\)g cũng bé hơn mức yêu cầu 3g nên có thể kết luận máy hoạt động đúng tiêu chuẩn mong muốn.
