
Trong 30 ngày, một nhà đầu tư đã theo dõi giá cổ phiếu của hai công ty G và H vào phiên mở cửa mỗi ngày. Thông tin được ghi lại ở hai bảng dưới đây:
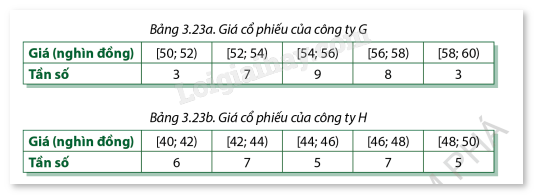
Giá cổ phiếu của công ty nào ít biến động hơn (làm tròn kết quả đến hàng phần trăm)?

Áp dụng các công thức sau để tính độ lệch chuẩn giá cổ phiếu của công ty G và H. Sau đó lấy hai giá trị này đem so sánh, công ty nào có độ lệch chuẩn thấp hơn thì giá cổ phiếu của công ty đó ít biến động hơn.
- Công thức tính trung bình:
\(\overline x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\overline x } \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\overline x } \right)}^2}} \)

Theo đề bài, ta có N = 30.
Công ty G:

- Giá cổ phiếu trung bình là:
Advertisements (Quảng cáo)
\({\bar x_G} = \frac{{51.3 + 53.7 + 55.9 + 57.8 + 59.3}}{{30}} \approx 55,07\)
- Tính \(\overline {x_G^2} \):
\(\overline {x_G^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{51}^2}.3 + {{53}^2}.7 + {{55}^2}.9 + {{57}^2}.8 + {{59}^2}.3}}{{30}} \approx 3037,53\)
- Độ lệch chuẩn giá cổ phiếu của công ty G là:
\({S_G} = \sqrt {\overline {x_G^2} - {{\left( {{{\overline x }_G}} \right)}^2}} = \sqrt {3037,53 - 55,{{07}^2}} \approx 2,197\)
Công ty H:

- Giá cổ phiếu trung bình là:
\({\bar x_H} = \frac{{41.6 + 43.7 + 45.5 + 47.7 + 49.5}}{{30}} \approx 44,87\)
- Tính \(\overline {x_H^2} \):
\(\overline {x_H^2} = \frac{{\sum {{f_i}.x_i^2} }}{N} = \frac{{{{41}^2}.6 + {{43}^2}.7 + {{45}^2}.5 + {{47}^2}.7 + {{49}^2}.5}}{{30}} \approx 2020,73\)
- Độ lệch chuẩn giá cổ phiếu của công ty G là:
\({S_H} = \sqrt {\overline {x_H^2} - {{\left( {{{\overline x }_H}} \right)}^2}} = \sqrt {2020,73 - 44,{{87}^2}} \approx 2,777\)
Vì \({S_G}
