
Bạn Mai dự định đăng kí xét tuyển vào đại học các ngành khối A00 (thi Toán, Vật lí, Hoá học) và A01 (thi Toán, Vật lí, Tiếng Anh). Bạn tìm hiểu điểm chuẩn năm trước của một số trường đóng trên những địa bàn không quá xa nơi gia đình mình sinh sống. Thông tin bạn thu được là:
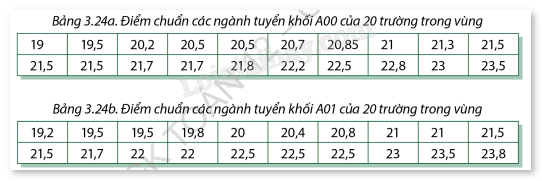
a) Lập mẫu số liệu ghép nhóm cho hai mẫu số liệu bạn Mai thu thập được, với độ dài các nhóm ghép là 1 và nhóm đầu tiên là [19; 20).
b) Những trường mà bạn Mai tìm hiểu có điểm chuẩn khối nào ổn định hơn?

a) Lập bảng với các nhóm ghép bắt đầu từ [19; 20), [20; 21), ….
b) Áp dụng các công thức sau để tính độ lệch chuẩn điểm chuẩn của hai khối. Khối nào có độ lệch chuẩn thấp hơn thì điểm chuẩn khối đó ổn định hơn
- Công thức tính trung bình:
\(\bar x = \frac{{\sum\limits_{i = 1}^k {\left( {{x_i}{f_i}} \right)} }}{N}\)
- Công thức tính độ lệch chuẩn:
\(S = \sqrt {\overline {{x^2}} - {{\left( {\bar x} \right)}^2}} = \sqrt {\frac{{\sum {{f_i}x_i^2} }}{N} - {{\left( {\bar x} \right)}^2}} \)

a) Theo đề bài, ta có N = 20.
Khối A00:
Advertisements (Quảng cáo)
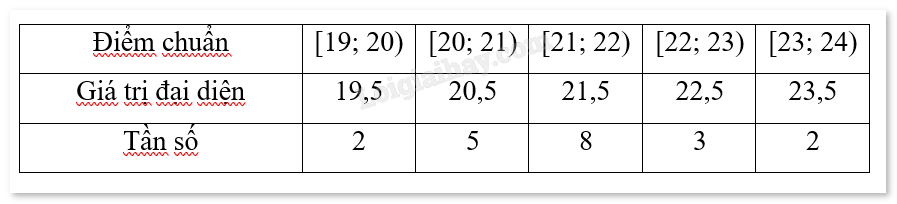
Khối A01:
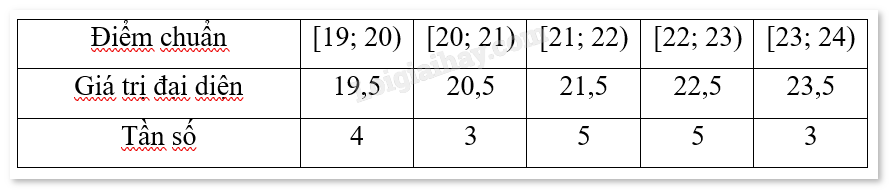
b)
Điểm chuẩn trung bình của hai khối là:
\(\overline {{x_{A00}}} = \frac{{19,5.2 + 20,5.5 + 21,5.8 + 22,5.3 + 23,5.2}}{{20}} = 21,4\)
\(\overline {{x_{A01}}} = \frac{{19,5.4 + 20,5.3 + 21,5.5 + 22,5.5 + 23,5.3}}{{20}} = 21,5\)
Tính \(\overline {x_{A00}^2} ,\overline {x_{A01}^2} \):
\(\overline {x_{A00}^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{19,{5^2}.2 + 20,{5^2}.5 + 21,{5^2}.8 + 22,{5^2}.3 + 23,{5^2}.2}}{{20}} = 459,15\)
\(\overline {x_{A01}^2} = \frac{{\sum {{f_i}x_i^2} }}{N} = \frac{{19,{5^2}.4 + 20,{5^2}.3 + 21,{5^2}.5 + 22,{5^2}.5 + 23,{5^2}.3}}{{20}} = 464,05\)
Độ lệch chuẩn của hai khối là:
\({S_{A00}} = \sqrt {\overline {x_{A00}^2} - {{\left( {\overline {{x_{A00}}} } \right)}^2}} = \sqrt {459,15 - 21,{4^2}} \approx 1,091\)
\({S_{A01}} = \sqrt {\overline {x_{A01}^2} - {{\left( {\overline {{x_{A01}}} } \right)}^2}} = \sqrt {464,05 - 21,{5^2}} \approx 1,342\)
Khối A00 có độ lệch chuẩn thấp hơn, nghĩa là điểm chuẩn khối A00 ổn định hơn so với khối A01.
