Câu 1
Dựa vào hình ảnh dưới đây, thực hiện các yêu cầu.

a) Viết tổng các số hạng bằng nhau để tìm khối lượng cam của 7 túi.
b) Viết phép nhân để tìm khối lượng cam của 7 túi.
c) Số?

d) Nêu tên các thành phần của mỗi phép tính ở câu c.
e) Nêu cách tìm thành phần chưa biết trong mỗi phép tính sau.
1,5 x .?. = 10,5
.?. : 7 = 10,5
10,5 : .?. = 7

Đọc yêu cầu và trả lời các câu hỏi.

a) Tổng các số hạng bằng nhau để tìm khối lượng cam của 7 túi là: 2 + 2 + 2 + 2 + 2 + 2 + 2 =14 (kg)
b) Phép nhân để tìm khối lượng cam của 7 túi là: 2 x 7 = 14 (kg)
c)

d)
|
2 x 7 = 14 |
14 : 7 = 2 |
14 : 2 = 7 |
|
Trong đó: 2 là thừa số 7 là thừa số 14 là tích |
Trong đó: 14 là số bị chia 7 là số chia 2 là thương |
Trong đó: 14 là số bị chia 2 là số chia 7 là thương |
e) 1,5 x .?. = 10,5
Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết
.?. : 7 = 10,5
Muốn tìm số bị chia ta lấy thương nhân với số chia
10,5 : .?. = 7
Muốn tìm số chia ta lấy số bị chia chia cho thương
Câu 2
a) Số?
Chia đều 78 quyển vở cho 35 bạn, mỗi bạn được .?. quyển, còn dư .?. quyển.
b) Nêu tên các thành phần của phép chia có dư sau.
78 : 35 = 2 (dư 8)
Chú ý: Trong phép chia có dư, số dư phải bé hơn số chia.

Dựa vào kiến thức đã học và trả lời câu hỏi.

a) Ta có: 75 : 35 = 2 (dư 5)
Vậy chia đều 78 quyển vở cho 35 bạn, mỗi bạn được 2 quyển, còn dư 5 quyển.
b) 78 : 35 = 2 (dư 8)
Trong đó:
75 là số bị chia
35 là số chia
2 là thương
8 là số dư
Câu 3
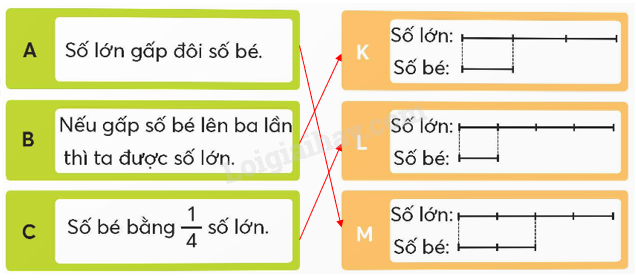
Chọn sơ đồ phù hợp với sự liên quan giữa số lớn và số bé.
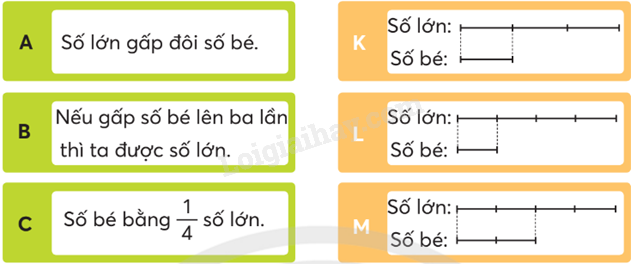

Dựa vào kiến thức đã học và chọn sơ đồ phù hợp với sự liên quan giữa số lớn và số bé.

Câu 4
Thay .?. bằng chữ hoặc số thích hợp.
a) Phép nhân các số tự nhiên, phân số, số thập phân đều có các tính chất sau:
- Tính chất giao hoán: a x b = .?. x a
- Tính chất kết hợp: (a x b) x c = a x (.?. x c)
- Nhân một tổng với một số: (a + b) x c = a x c + .?. x c
- Nhân với 1: a x 1 = 1 x .?. = .?.
b) Các phép nhân, phép chia đặc biệt:
- a x 0 = 0 x a = .?.
- a : 1 = .?.
- a : .?. = 1 (a khác 0)
- 0 : b = .?. (b khác 0)
c) Không có phép chia cho số .?.

Điền chữ hoặc số thích hợp vào chỗ chấm.

a) Phép nhân các số tự nhiên, phân số, số thập phân đều có các tính chất sau:
- Tính chất giao hoán: a x b = b x a
- Tính chất kết hợp: (a x b) x c = a x (b x c)
- Nhân một tổng với một số: (a + b) x c = a x c + b x c
- Nhân với 1: a x 1 = 1 x a = a
b) Các phép nhân, phép chia đặc biệt:
- a x 0 = 0 x a = 0
- a : 1 = a
- a : a = 1 (a khác 0)
- 0 : b = 0 (b khác 0)
c) Không có phép chia cho số 0
Câu 5
Tính nhẩm.
a) 127 x 100
0,83 x 10
5,64 x 1 000
b) 36 000 : 100
4,2 : 10
788 : 1000

- Khi nhẩm nhẩm một số tự nhiên với 10, 100, 1 000, .... ta viết thêm một, hai, ba, ... chữ số 0 vào bên phải số đó
- Khi chia nhẩm số tròn chục, tròn trăm, tròn nghìn, .... cho 10, 100, 1 000, .... ta bớt đi một, hai, ba, ... chữ số 0 ở bên phải số đó.

a) 127 x 100 = 12 700
0,83 x 10 = 8,3
5,64 x 1 000 = 5640
b) 36 000 : 100 = 360
4,2 : 10 = 0,42
788 : 1000 = 0,788
Câu 6
a) Hoàn thiện các câu sau.
- Khi nhân một số với 0,1; 0,01; … ta có thể lấy số đó chia cho .?., .?. , …
- Khi chia một số cho 0,1; 0,01;… ta có thể lấy số đó nhân với .?. , .?. , …
b) Tính
8,6 x 0,1
14,1 x 0,01
572 x 0,001
8,6 : 0,1
14,1 : 0,01
572 : 0.001

- Muốn nhân một số thập phân với 0,1; 0,01; 0,001; ... ta chỉ việc chuyển dấu phẩy của số đó tương ứng sang bên trái một, hia, ba, ... chữ số.
- Muốn chia một số thập phân cho 0,1; 0,01; 0,001; ... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số.

a)
- Khi nhân một số với 0,1; 0,01; … ta có thể lấy số đó chia cho 10, 100, …
- Khi chia một số cho 0,1; 0,01;… ta có thể lấy số đó nhân với 10, 100, …
b) 8,6 x 0,1 = 0,86
8,6 : 0,1 = 86
14,1 x 0,01 = 0,141
14,1 : 0,01 = 1410
572 x 0,001 = 0,572
572 : 0,001 = 572 000
Câu 7
a) Nhân hay chia?
- Khi nhân một số với 0,5; 0,25 ta có thể lấy số đó .?. cho 2;4.
- Khi chia một số cho 0,5; 0,25 ta có thể lấy số đó .?. với 2; 4.
b) Tính
12 x 0,5
320 x 0,25
1,5 : 0,5
$\frac{3}{8}$ : 0,25

- Khi nhân một số với 0,5; 0,25 ta có thể lấy số đó chia cho 2;4.
Advertisements (Quảng cáo)
- Khi chia một số cho 0,5; 0,25 ta có thể lấy số đó nhân với 2; 4.

a) - Khi nhân một số với 0,5; 0,25 ta có thể lấy số đó chia cho 2;4.
- Khi chia một số cho 0,5; 0,25 ta có thể lấy số đó nhân với 2; 4.
b) 12 x 0,5 = 6
320 x 0,25 = 80
1,5 : 0,5 = 3
$\frac{3}{8}$ : 0,25 = 1,5
Câu 8
Tính bằng cách thuận.
a) 0,25 x 8,1 x 40
0,9 x 20 x 0,5
b) 40 x 0,2 x 0,25 x 50
2,6 x 1,7 + 7,4 x 1,7

- Áp dụng tính chất giao hoán, kết hợp của phép cộng để nhóm các số có tổng là số tròn trăm, tròn nghìn, ….

a) 0,25 x 8,1 x 40
= (0,25 x40) x 8,1
= 10 x 8,1
= 81
0,9 x 20 x 0,5
= 0,9 x (20 x 0,5)
= 0,9 x 10
= 9
b) 40 x 0,2 x 0,25 x 50
= (40 x 0,25) x (0,2 x 50)
= 10 x 10
= 100
2,6 x 1,7 + 7,4 x 1,7
= (2,6 + 7,4) x 1,7
= 10 x 1,7
= 17
Câu 9
Viết kết quả phép chia dưới dạng phân số và số thập phân.
Mẫu: 1 : 2 = $\frac{1}{2}$ = 0,5
a) 5 : 2
b) 2 : 5
c) 3 : 4
d) 1 : 8

Thực hiện theo mẫu.

a) 5 : 2 = $\frac{5}{2} = 2,5$
b) 2 : 5 = $\frac{2}{5}$ = 0,4
c) 3 : 4 = $\frac{3}{4}$ = 0,75
d) 1 : 8 = $\frac{1}{8} = $0,125
Câu 10
Thực hiện phép chia rồi thử lại.

a) 4 544 : 71
b) 2 045 : 58
c) 8,64 : 3,6
d) 279 : 4,5

Thực hiện theo mẫu.


Câu 11
Tính giá trị của biểu thức.
a) 21 327 – 209 x 5
b) 5,25 : 3 x 4
c) $\frac{5}{7} \times \left( {\frac{1}{2} + \frac{1}{5}} \right)$
d) $\frac{2}{3}:\frac{1}{4} - \frac{1}{2}:\frac{1}{4}$

- Trong biểu thức chứa các phép tính cộng, phép trừ, phép nhân, phép chia thì ta thực hiện nhân chia trước, cộng trừ sau.
- Thực hiện trong ngoặc trước, ngoài ngoặc sau.
- Trong biểu thức có chứa phép nhân, phép chia thì ta thực hiện từ trái qua phải
- Áp dụng tính chất giao hoán và kết hợp.

a) 21 327 – 209 x 5
= 21 327 – 1 045
= 20 282
b) 5,25 : 3 x 4
= 1,75 x 4
= 7
c) $\frac{5}{7} \times \left( {\frac{1}{2} + \frac{1}{5}} \right)$
= $\frac{5}{7} \times \left( {\frac{5}{{10}} + \frac{2}{{10}}} \right)$
= $\frac{5}{7} \times \frac{7}{{10}} = \frac{5}{{10}} = \frac{1}{2}$
d) $\frac{2}{3}:\frac{1}{4} - \frac{1}{2}:\frac{1}{4}$
= $\left( {\frac{2}{3} - \frac{1}{2}} \right):\frac{1}{4}$
= $\left( {\frac{4}{6} - \frac{3}{6}} \right):\frac{1}{4}$
= $\frac{1}{6} \times 4 = \frac{2}{3}$
Câu 12
Chọn ý trả lời đúng.
a) $\frac{3}{5}$: .?. = $\frac{1}{5}$. Số thích hợp thay vào .?. là:
A. $\frac{2}{5}$
B. $\frac{4}{5}$
C. $\frac{3}{{25}}$
D. 3
b) Tỉ số phần trăm của 0,66 kg và 2,4 kg là:
A. 0,275
B. 27,5
C. 27,5%
D. 27,5% kg

a) Muốn tìm số chia ta lấy số bị chia chia cho thương
b) Muốn tìm tỉ số phần trăm của hai số a và b, ta làm như sau:
- Tìm thương của a và b.
- Nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.

a) $\frac{3}{5}:.?. = \frac{1}{5}$
.?. = $\frac{3}{5}:\frac{1}{5} = 3$
Chọn D
b) Ta có: 0,66 : 2,4 = 0,275 = 27,5%
Vậy tỉ số phần trăm của 0,66 kg và 2,4 kg là 27,5%
Chọn C
Câu 13
Có 600 học sinh các khối 1, 2 và 3 đi tham quan, trong đó có $\frac{2}{5}$ số học sinh là học sinh lớp 3; 45% số học sinh còn lại là lớp 2. Hỏi có bao nhiêu học sinh lớp 1 đi tham quan?

- Tính số học sinh lớp 3 đi tham quan
- Tính số học sinh lớp 2 đi tham quan
- Tính số học sinh lớp 1 đi tham quan

Số học sinh lớp 3 đi tham quan là:
600 x $\frac{2}{5}$= 240 (học sinh)
Ta có: 45% = $\frac{9}{{20}}$
Số học sinh lớp 2 đi tham quan là:
600 x $\frac{9}{{20}}$ = 270 (học sinh)
Số học sinh lớp 1 đi tham quan là:
600 – 240 – 270 = 90 (học sinh)
Đáp số: 90 học sinh
Hoạt động thực tế
Số?
Dưới đây là hình ảnh gia đình bạn Hòa, sống tại Thành phố Hồ Chí Minh. Nếu cả gia đình Hòa đi Hà Nội bằng máy bay thì tiền vé hết tất cả là .?. đồng.


- Tính số tiền gia đình Hòa phải chi trả giá vé một chiều
- Tính tổng số tiền gia đình Hòa phải chi trả cho cả lượt đi và lượt về

Giá vé một chiều cả gia đình Hòa đi Hà Nội bằng máy bay phải chi hết số tiền là:
(2 479 000 x 4) + 326 000 + 2 243 000 = 12 485 000 (đồng)
Gia đình bạn Hòa chi tiền vé hết tất cả số tiền là:
12 485 000 x 2 = 24 970 000 (đồng)
Đáp số: 24 970 000 đồng
Đất nước em
Số?
Tham quan một làng nghề, Hòa thấy mỗi thân tre được cưa thành 12 khúc, mỗi khúc tre được xẻ thành 12 thanh. Vậy, từ 1 thân tre sẽ có .?. thanh.

Số thanh ở thân tre = số khúc ở mỗi thân tre x số thanh ở mỗi khúc

Thân tre có số thanh là:
12 x 12 = 144 (thanh)
Đáp số: 144 thanh
