Hoạt động 1 Câu 1
Trả lời câu hỏi 1 trang 99 SGK Toán 4 Kết nối tri thức
Trong các hình dưới đây, hình nào là hình thang?
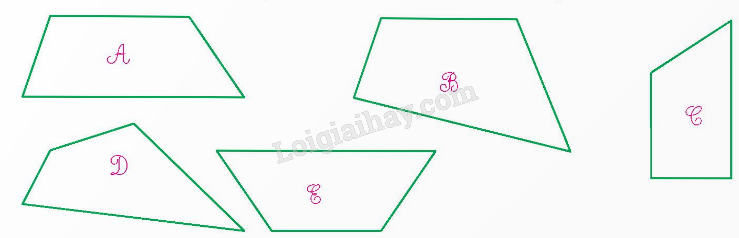

Hình thang có một cặp cạnh đối diện song song.

Các hình là hình thang: Hình A, Hình C và hình E.
Hoạt động 1 Câu 2
Trả lời câu hỏi 2 trang 99 SGK Toán 4 Kết nối tri thức
Dưới đây là một số hình ảnh thực tế có dạng hình thang. Em hãy tìm thêm một số hình ảnh thực tế có dạng hình thang.


Em tìm thêm một số hình ảnh thực tế có dạng hình thang.

Một số hình ảnh thực tế có dạng hình thang: cái thang, túi xách, ...


Hoạt động 2 Câu 3
Trả lời câu hỏi 3 trang 99 SGK Toán 4 Kết nối tri thức
a) Hình thang vuông.
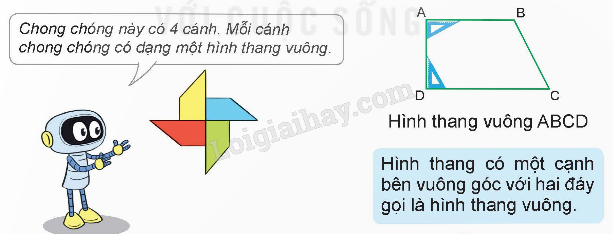
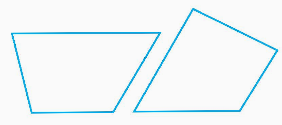
b) Sử dụng ê ke để kiểm tra xem mỗi hình thang bên có phải là hình thang vuông không.

Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.

Mỗi hình thang bên không phải là hình thang vuông.
Hoạt động 2 Câu 1
Trả lời câu hỏi 1 trang 100 SGK Toán 4 Kết nối tri thức
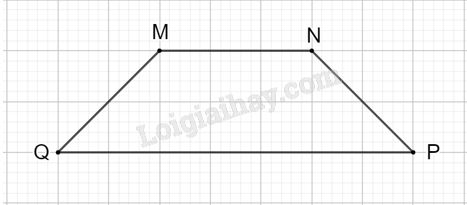
Vẽ hình thang MNPQ với MN và QP là hay đáy (trên giấy kẻ ô vuông).

- Vẽ đoạn thẳng MN.
- Vẽ đoạn thẳng QP song song với đoạn thẳng MN.
- Nối M với Q và N với P ta được hình thang MNPQ với hai đáy là MN và QP.

Hoạt động 2 Câu 2
Trả lời câu hỏi 2 trang 100 SGK Toán 4 Kết nối tri thức
Cho hình vẽ:
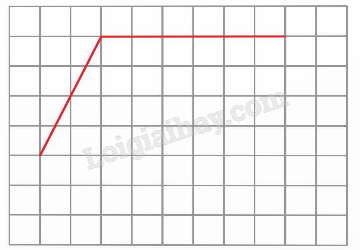
Thực hiện yêu cầu vẽ thêm hai đoạn thẳng vào hình vẽ để được một hình thang, Mai và Việt đã làm như sau:
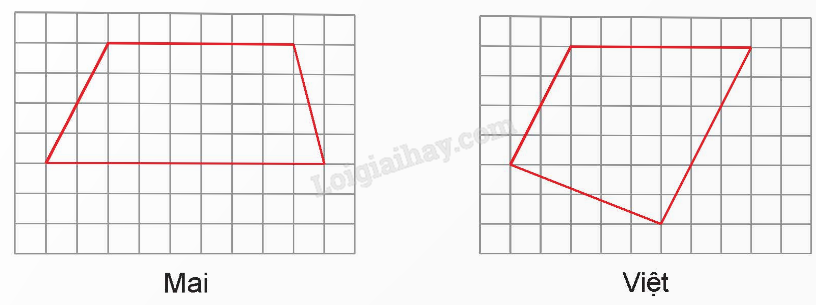
Hỏi bạn nào thực hiện đúng yêu cầu?

Hình thang có một cặp cạnh đối diện song song.

Bạn Mai thực hiện đúng yêu cầu.
Hoạt động 2 Câu 3
Trả lời câu hỏi 3 trang 101 SGK Toán 4 Kết nối tri thức
Vẽ hình (theo mẫu).
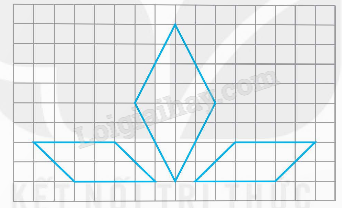

HS vẽ theo mẫu.

Học sinh tự thực hiện.
Hoạt động 2 Câu 4
Trả lời câu hỏi 4 trang 101 SGK Toán 4 Kết nối tri thức
a) Vẽ hình (theo mẫu).
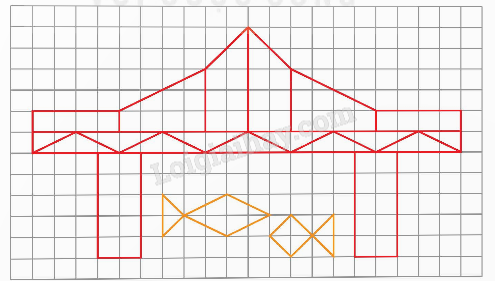
b) Tô màu trang trí hình em vừa vẽ được ở câu a.

HS vẽ theo mẫu.

Học sinh tự thực hiện
Hoạt động 3 Câu 1
Trả lời câu hỏi 3 trang 103 SGK Toán 4 Kết nối tri thức
Tính diện tích hình thang, biết:
a) Độ dài hai đáy lần lượt là 4 cm và 6cm; chiều cao là 3 cm.
b) Độ dài hai đáy lần lượt là 11 cm và 9 cm; chiều cao là 8 cm.

Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó:
S là diện tích;
a, b là độ dài các cạnh đáy;
h là chiều cao.

a) Diện tích hình thang là:
$\frac{{\left( {6 + 4} \right) \times 3}}{2} = 15\left( {c{m^2}} \right)$
b) Diện tích của hình thang là:
$\frac{{\left( {11 + 9} \right) \times 8}}{2} = 80\;\left( {c{m^2}} \right)$
Đáp số: a) 15 cm2
b) 80 cm2
Hoạt động 3 Câu 2
Trả lời câu hỏi 2 trang 103 SGK Toán 4 Kết nối tri thức
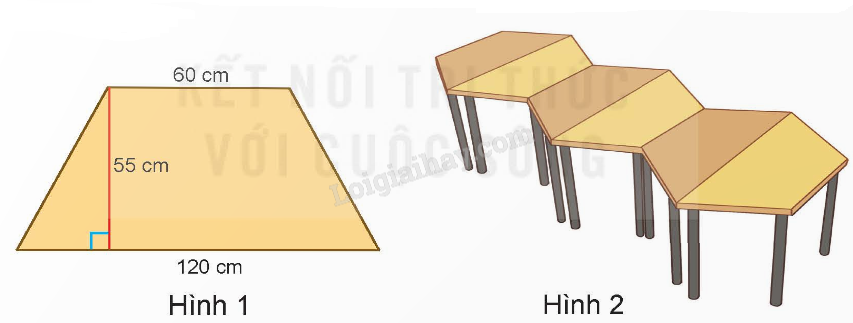
Dùng 6 cái bàn giống nhau với mặt bàn hình thang có kích thước như hình 1 để ghép thành một bàn đa năng như hình 2. Tính diện tích mặt bàn đa năng.

Advertisements (Quảng cáo)
- Tìm diện tích mặt bàn hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Diện tích mặt bàn đa năng = diện tích hình thang x 6

Diện tích mặt bàn hình thang là:
$\frac{{\left( {120 + 60} \right) \times 55}}{2} = 4\;950\;\left( {c{m^2}} \right)$
Diện tích mặt bàn đa năng như hình 2 là:
4 950 x 6 = 29 700 (cm2)
Đáp số: 29 700 cm2
Hoạt động 3 Câu 3
Trả lời câu hỏi 3 trang 103 SGK Toán 4 Kết nối tri thức
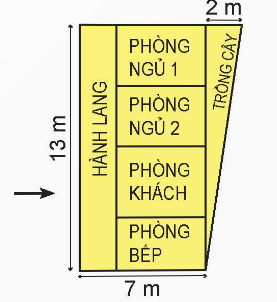
a) Hình bên là bản vẽ thiết kế một ngôi nhà trên mảnh đất có dạng hình thang vuông. Tính diện tích mảnh đất đó.
b) Với mảnh đất như vậy, hãy thiết kế lại các phòng theo ý thích của em.

- Tìm chiều dài mảnh đất
- Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó:
S là diện tích;
a, b là độ dài các cạnh đáy;
h là chiều cao.

a) Chiều dài mảnh đất là:
7 + 2 = 9 (m)
Diện tích mảnh đất đó là:
$\frac{{(9 + 7) \times 13}}{2} = 104$ (m2)
Đáp số: 104 m2
b) Học sinh tự thực hiện
Luyện tập Câu 1
Trả lời câu hỏi 1 trang 104 SGK Toán 4 Kết nối tri thức
Tính diện tích hình thang có độ dài hay đáy lần lượt là a và b; chiều cao là h được cho như bảng dưới đây:
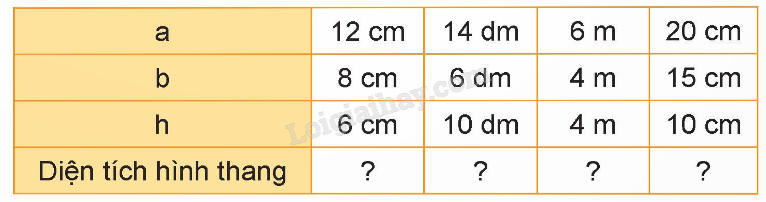

Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó: S là diện tích; a, b là độ dài hai đáy; h là chiều cao.

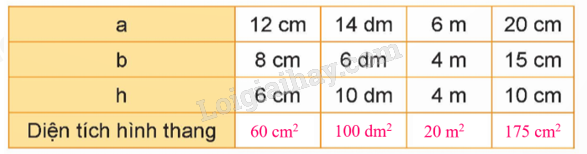
Diện tích hình thang có a = 12 cm, b = 8 cm, h = 6 cm là: $\frac{{(12 + 8) \times 6}}{2} = 60$ (cm2)
Diện tích hình thang có a = 14 dm, b = 6 dm, h = 10 dm là: $\frac{{(14 + 6) \times 10}}{2} = 100$ (dm2)
Diện tích hình thang có a = 6 m, b = 4 m, h = 4 m là: $\frac{{(6 + 4) \times 4}}{2} = 20$ (m2)
Diện tích hình thang có a = 20 cm, b = 15 cm, h = 10 cm là: $\frac{{(20 + 15) \times 10}}{2} = 175$ (cm2)
Luyện tập Câu 2
Trả lời câu hỏi 2 trang 104 SGK Toán 4 Kết nối tri thức
Chọn câu trả lời đúng.
Diện tích hình thang có độ dài hai đáy lần lượt là 25 cm và 15 cm; chiều cao 1 dm là:
A. 4 cm2
B. 2 cm2
C. 2 dm2
D. 4 dm2

Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó: S là diện tích; a, b là độ dài hai đáy; h là chiều cao.

Đổi 1 dm = 10 cm
Diện tích hình thang là: $\frac{{\left( {25 + 15} \right) \times 10}}{2} = 200\;$(cm2)= 2 dm2
Chọn đáp án C.
Luyện tập Câu 3
Trả lời câu hỏi 3 trang 104 SGK Toán 4 Kết nối tri thức
Tính diện tích con thuyền như hình dưới đây, biết rằng mỗi ô vuông có cạnh dài 1 cm.
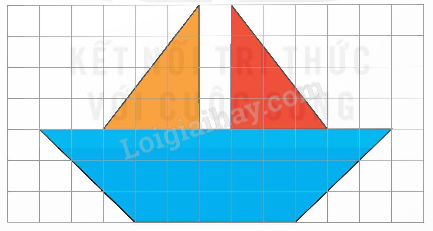

- Tính diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
- Diện tích con thuyền = Diện tích hình thang + diện tích hình tam giác x 2

Diện tích hình tam giác vuông có độ dài hai cạnh góc vuông là 3 cm và 4 cm là:
$\frac{{3 \times 4}}{2} = 6\left( {c{m^2}} \right)$
Diện tích hình thang có chiều dài 11 cm, chiều rộng 5 cm, chiều cao 3 cm là:
\[\frac{{\left( {11 + 5} \right) \times 3}}{2} = 24\left( {c{m^2}} \right)\]
Diện tích con thuyền là:
6 x 2 + 24 = 36 (cm2)
Đáp số: 36 cm2
Luyện tập Câu 4
Trả lời câu hỏi 4 trang 104 SGK Toán 4 Kết nối tri thức
Một mảnh đất dạng hình thang có độ dài hai đáy là 35 m và 15 m, chiều cao là 20 m. Tính số tiền mua cỏ để vừa đủ phủ kín mảnh đất đó, biết rằng mỗi mét vuông cỏ có giá tiền là 45 000 đồng.


- Diện tích hình thang: $S = \frac{{\left( {a + b} \right) \times h}}{2}$
Trong đó S là diện tích; a, b là độ dài hai đáy; h là chiều cao.
- Số tiền mua cỏ = số tiền mỗi mét vuông cỏ x diện tích mảnh đất

Diện tích mảnh đất là:
$\frac{{\left( {35 + 15} \right) \times 20}}{2} = 500\;\left( {{m^2}} \right)$
Số tiền mua cỏ để vừa đủ phủ kín mảnh đất là:
45 000 x 500 = 22 500 000 (đồng)
Đáp số: 22 500 000 đồng.
