Hoạt động Câu 1
Trả lời câu hỏi 1 trang 13
Trên bãi cỏ có 49 con bò sữa gồm bò vàng và bò khoang, trong đó số bò khoang bằng $\frac{2}{5}$số bò vàng. Hỏi trên bãi cỏ có bao nhiêu con bò khoang, bao nhiêu con bò vàng?


1. Tìm tổng số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số - số bé).
Chú ý: Có thể làm gộp bước 1 và bước 2

Ta có sơ đồ:
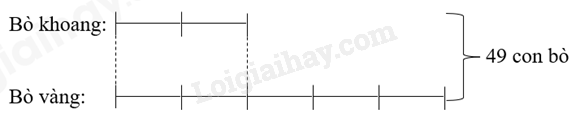
Tổng số phần bằng nhau là:
2 + 5 = 7 (phần)
Số bò khoang là:
49 : 7 x 2 = 14 (con)
Số bò vàng là:
49 - 14 = 35 (con)
Đáp số: Số bò khoang là 14 con;
Số bò vàng là 35 con.
Hoạt động Câu 2
Trả lời câu hỏi 2 trang 13
Trong một ngày, một cửa hàng đã bán hàng và thu được số tiền là 18 000 000 đồng. Biết số tiền bán được trong buổi sáng bằng $\frac{3}{2}$số tiền bán được trong buổi chiều. Hỏi số tiền bán được trong mỗi buổi là bao nhiêu?

1. Tìm tổng số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số - số bé).
Chú ý: Có thể làm gộp bước 1 và bước 2

Ta có sơ đồ:
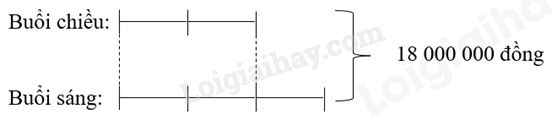
Tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Số tiền bán được trong buổi chiều là:
18 000 000 : 5 x 2 = 7 200 000 (đồng)
Số tiền bán được trong buổi sáng là:
18 000 000 – 7 200 000 = 10 800 000 (đồng)
Đáp số: Số tiền buổi chiều là 7 200 000 đồng;
Số tiền buổi sáng là 10 800 000 đồng.
Luyện tập Câu 1
Trả lời câu hỏi 1 trang 13
Đường từ nhà đến trường, bạn Páo qua một đoạn đường dài 1 400 m gồm đoạn lên dốc và đoạn xuống dốc. Biết độ dài đoạn lên dốc bằng $\frac{3}{4}$ độ dài đoạn xuống dốc. Hỏi mỗi đoạn lên dốc, xuống dốc dài bao nhiêu mét?


1. Tìm tổng số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số - số bé).
Chú ý: Có thể làm gộp bước 1 và bước 2

Ta có sơ đồ:
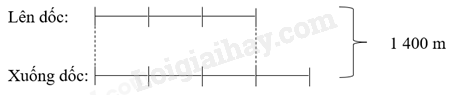
Tổng số phần bằng nhau là:
3 + 4 = 7 (phần)
Đoạn lên dốc dài số mét là:
1 400 : 7 x 3 = 600 (m)
Đoạn xuống dốc dài số mét là:
1 400 - 600 = 800 (m)
Đáp số: Đoạn lên dốc là 600 m;
Đoạn xuống dốc là 800 m.
Luyện tập Câu 2
Trả lời câu hỏi 2 trang 14
Trong một gian hàng siêu thị điện máy có 36 chiếc ti vi gồm ti vi 75 inch và ti vi 55 inch. Tìm số ti vi mỗi loại, biết số ti vi 55 inch gấp 3 lần số ti vi 75 inch.

1. Tìm tổng số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số - số bé).
Advertisements (Quảng cáo)
Chú ý: Có thể làm gộp bước 1 và bước 2

Ta có sơ đồ:
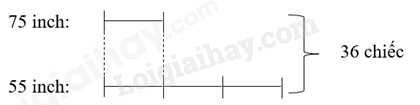
Tổng số phần bằng nhau là:
3 + 1 = 4 (phần)
Số ti vi 75 inch là:
36 : 4 x 1 = 9 (chiếc)
Số ti vi 55 inch là:
36 – 9 = 27 (chiếc)
Đáp số: Số ti vi 75 inch là 9 chiếc;
Số ti vi 55 inch là 27 chiếc.
Luyện tập Câu 3
Trả lời câu hỏi 3 trang 14
Rô-bốt, Việt và Mai đi tham quan trại chăn nuôi gà và vịt. Bác chủ trại cho biết cả gà và vịt có 34 000 con, số con gà bằng $\frac{7}{{10}}$số con vịt. Hỏi số gà ít hơn số vịt bao nhiêu con?


1. Tìm tổng số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số - số bé).
Chú ý: Có thể làm gộp bước 1 và bước 2

Ta có sơ đồ:

Tổng số phần bằng nhau là:
7 + 10 = 17 (phần)
Số gà là:
34 000 : 17 x 7 = 14 000 (con)
Số vịt là:
34 000 – 14 000 = 20 000 (con)
Đáp số: Số gà là 14 000 con;
Số vịt là 20 000 con.
Luyện tập Câu 4
Trả lời câu hỏi 4 trang 14
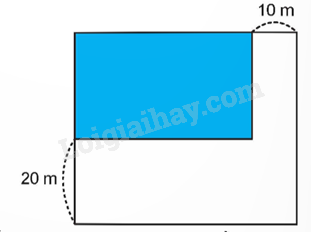
Một mảnh đất dạng hình chữ nhật có chu vi 130 m và chiều rộng bằng $\frac{5}{8}$chiều dài. Người ta mở chiều dài thêm 10 m, chiều rộng thêm 20 m để được mảnh đất dạng hình chữ nhật mới (như hình vẽ). Tính:
a) Chiều dài và chiều rộng mảnh đất dạng hình chữ nhật ban đầu.
b) Diện tích mảnh đất dạng hình chữ nhật mới.

a)
1. Tìm tổng số phần bằng nhau.
2. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
3. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
4. Tìm số lớn (lấy tổng hai số - số bé).
Chú ý: Có thể làm gộp bước 1 và bước 2
b)
1. Chiều dài sau khi mở rộng = chiều dài ban đầu + 10.
2. Chiều rộng sau khi mở rộng = chiều rộng ban đầu + 20.
3. Diện tích mảnh đất dạng hình chữ nhật mới = chiều dài sau khi mở rộng x chiều rộng sau khi mở rộng.

a) Tổng chiều dài và chiều rộng là:
130 : 2 = 65 (m)
Ta có sơ đồ:

Tổng số phần bằng nhau là:
8 + 5 = 13 (phần)
Chiều rộng là:
65 : 13 x 5 = 25 (m)
Chiều dài là:
65 – 25 = 40 (m)
Đáp số: Chiều rộng là 25 m;
Chiều dài là 40 m.
b) Chiều dài sau khi mở rộng là:
25 + 10 = 35 (m)
Chiều rộng sau khi mở rộng là:
40 + 10 = 50 (m)
Diện tích mảnh đất dạng hình chữ nhật mới là:
35 x 50 = 1 750 (m2)
Đáp số: 1 750 m2
