Giải bài 3.4 trang 37 sách bài tập toán 7 - Kết nối tri thức với cuộc sống - Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc
Vẽ \(\widehat {xAm} = {50^0}\). Vẽ tia phân giác An của \(\widehat {xAm}\).
a) Tính \(\widehat {xAn}\).
b) Vẽ tia Ay là tia đối của tia An. Tính \(\widehat {mAy}\).
a) Tia phân giác của 1 góc nằm giữa 2 cạnh của góc và chia góc đó thành 2 góc bằng nhau.
b) Sử dụng tổng của hai góc kề bù bằng 180 độ.
Advertisements (Quảng cáo)
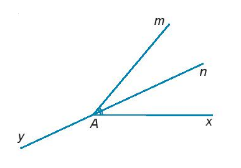
a)
Vì tia An là tia phân giác của \(\widehat {xAm}\) nên
\(\widehat {xAn} = \widehat {nAm} = \dfrac{{\widehat {xAm}}}{2} = \dfrac{{{{50}^0}}}{2} = {25^0}\)
Vậy \(\widehat {xAn} = {25^0}\).
b)
Ta có: \(\widehat {nAm} + \widehat {mAy} = {180^0}\) (hai góc kề bù)
\(\begin{array}{l} \Rightarrow {25^0} + \widehat {mAy} = {180^0}\\ \Rightarrow \widehat {mAy} = {180^0} - {25^0}\\ \Rightarrow \widehat {mAy} = {155^0}\end{array}\)