
a)Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại đỉnh A.
b)Cho đoạn thẳng AB. Hãy nêu một cách sử dụng kết quả của câu a để vẽ đường thẳng vuông góc với AB tại A (bằng thước và compa)

- MA = MB = MC
- Chỉ ra các tam giác cân và các góc bằng nhau
- Chứng minh góc A bằng 90 độ.

Advertisements (Quảng cáo)
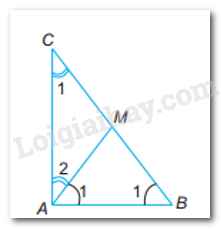
a) Ta có:MA = MB = MC (gt)
\( \Rightarrow \Delta MAB;\Delta MAC\) là hai tam giác cân tại đỉnh M
\( \Rightarrow \left\{ \begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}}\\\widehat {{A_2}} = \widehat {{C_1}}\end{array} \right.\)
Xét tam giác ABC:
\(\widehat A + \widehat B + \widehat C = {180^0}\) (Tổng 3 góc trong 1 tam giác)
\(\begin{array}{l} \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} + \widehat B + \widehat C = {180^0}\\ \Rightarrow \left( {\widehat {{A_1}} + \widehat B} \right) + \left( {\widehat {{A_2}} + \widehat C} \right) = {180^0}\\ \Rightarrow 2\widehat {{A_1}} + 2\widehat {{A_2}} = {180^0}\\ \Rightarrow \widehat {{A_1}} + \widehat {{A_2}} = {90^0}\end{array}\)
b)
Vẽ tam giác cân MAB rồi kéo dài BM về phía M đến điểm C sao cho MC = BM. Khi đó tam giác ABC vuông tại A.
