
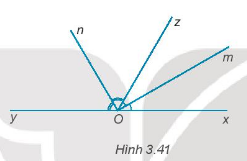
Cho góc bẹt xOy. Vẽ tia Oz sao cho \(\widehat {xOz} = {60^0}\). Vẽ tia Om là tia phân giác của góc xOz. Vẽ tia On là tia phân giác của góc zOy.
a)Tính số đo góc xOm.
b) Tính số đo góc yOn.
c) Tính số đo góc mOn.

a) Tia Om là tia phân giác của góc xOz
b)
-\(\widehat {yOz} + \widehat {zOx} = {180^0}\)
- Tia On là tia phân giác của góc yOn
c)
-\(\widehat {xOm} + \widehat {mOy} = {180^0}\)
- Tia On nằmg giữa hai tia Oy và Om
Advertisements (Quảng cáo)

a)
Ta có: Tia Om là tia phân giác của góc xOz
\( \Rightarrow \widehat {xOm} = \widehat {mOz} = \dfrac{{\widehat {xOz}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\)
Vậy \(\widehat {xOm} = {30^0}\).
b)
Ta có: \(\widehat {yOz} + \widehat {zOx} = {180^0}\)(hai góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {yOz} + {60^0} = {180^0}\\ \Rightarrow \widehat {yOz} = {180^0} - {60^0}\\ \Rightarrow \widehat {yOz} = {120^0}\end{array}\)
Tia On là tia phân giác của góc yOn nên \(\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\)
c)
Ta có: \(\widehat {xOm} + \widehat {mOy} = {180^0}\) (hai góc kề bù)
\( \Rightarrow {30^0} + \widehat {mOy} = {180^0} \Rightarrow \widehat {mOy} = {180^0} - {30^0} = {150^0}\)
Tia On nằm giữa hai tia Oy và Om nên:
\(\begin{array}{l}\widehat {yOn} + \widehat {nOm} = \widehat {yOm}\\ \Rightarrow {60^0} + \widehat {nOm} = {150^0}\\ \Rightarrow \widehat {nOm} = {150^0} - {60^0}\\ \Rightarrow \widehat {nOm} = {90^0}.\end{array}\)
