
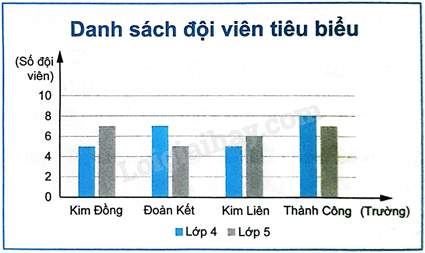
Biểu đồ bên thống kê số đội viên tiêu biểu của các trường tiểu học trên một thị trấn tham dự một buổi giao lưu. Chọn ngẫu nhiên 1 đội viên trong buổi giao lưu đó. Tính xác suất của các biến cố sau:
A: “Đội viên được chọn học lớp 5 trường Tiểu học Kim Đồng”;
B: “Đội viên được chọn học trường Tiểu học Đoàn Kết”;
C: “Đội viên được chọn học lớp 4”.

Sử dụng kiến thức về xác suất của biến cố để tính: Khi tất cả các kết quả của một trò chơi hay một phép thử đều có khả năng xảy ra bằng nhau thì xác suất của biến cố A là tỉ số giữa số kết quả thuận lợi cho A và tổng số kết quả có thể xảy ra của phép thử, tức là:
Advertisements (Quảng cáo)

Lưu ý: Để nhận biết các kết quả có cùng khả năng, chú ý đến các “từ khóa” liên quan đến phép thử: đồng xu, xúc xắc cân đối và đồng chất; các thẻ cùng loại, cùng kích thước; quả bóng, viên bi có cùng kích thước và khối lượng.

Tổng số đội viên tham gia buổi giao lưu là: \(5 + 7 + 7 + 5 + 5 + 6 + 8 + 7 = 50\)
Do đó, có 50 kết quả có cùng khả năng xảy ra đối với phép thử chọn ngẫu nhiên 1 đội viên trong buổi giao lưu đó.
Số các kết quả thuận lợi của biến cố A là 7. Xác suất của biến cố A là: \(P\left( A \right) = \frac{7}{{50}}\)
Số các kết quả thuận lợi của biến cố B là 12. Xác suất của biến cố B là: \(P\left( B \right) = \frac{{12}}{{50}} = \frac{6}{{25}}\)
Số các kết quả thuận lợi của biến cố C là 25. Xác suất của biến cố C là: \(P\left( C \right) = \frac{{25}}{{50}} = \frac{1}{2}\)
