
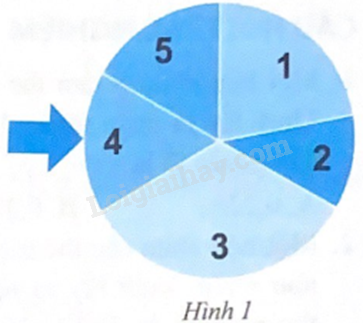
Cho tấm bìa như Hình 1. Thu xoay tấm bìa quanh tâm của nó và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Kết quả sau 150 lần xoay được ghi lại ở bảng sau:
|
Ô số |
1 |
2 |
3 |
4 |
5 |
|
Số lần |
36 |
12 |
54 |
Advertisements (Quảng cáo) 27 |
21 |
Hãy tính xác suất thực nghiệm của các biến cố:
A: “Mũi tên chỉ vào ô ghi số 1”;
B: “Mũi tên chỉ vào ô ghi số chẵn”;
C: “Mũi tên chỉ vào ô ghi số lớn hơn 3”.

Sử dụng kiến thức về xác suất thực nghiệm của biến cố: Gọi P(A) là xác suất xuất hiện biến cố A khi thực hiện một phép thử. Gọi m(A) là số lần xuất hiện biến cố A khi thực hiện một phép thử đó m lần. Xác suất thực nghiệm của biến cố A là tỉ số \(\frac{{m\left( A \right)}}{m}\).

Vì có 36 lần xảy ra biến cố A trong 150 lần thử nên xác suất thực nghiệm của các biến cố A sau 150 lần thử là: \(\frac{{36}}{{150}} = 0,24\)
Vì có \(12 + 27 = 39\) lần xảy ra biến cố B trong 150 lần thử nên xác suất thực nghiệm của các biến cố B sau 150 lần thử là: \(\frac{{39}}{{150}} = 0,26\)
Vì có \(27 + 21 = 48\) lần xảy ra biến cố C trong 150 lần thử nên xác suất thực nghiệm của các biến cố C sau 150 lần thử là: \(\frac{{48}}{{150}} = 0,32\)
