
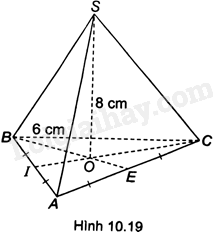
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 6cm, chiều cao 8cm như Hình 10.19. Tính thể tích hình chóp, biết \(\sqrt {27} \approx 5,2\)

Sử dụng kiến thức về thể tích của hình chóp tam giác đều: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.

Advertisements (Quảng cáo)
Kẻ các đường cao IC, BE của tam giác đều ABC. Gọi O là giao điểm của BE và IC, khi đó SO là đường cao của hình chóp tam giác đều S.ABC.
Tam giác ABC là tam giác đều nên \(AB = BC = 6cm\), CI là đường cao đồng thời là đường trung tuyến. Do đó, \(BI = \frac{1}{2}AB = 3cm\).
Áp dụng định lí Pythagore vào tam giác CBI vuông tại I có: \(B{I^2} + I{C^2} = B{C^2}\)
\(I{C^2} = B{C^2} - B{I^2} = {6^2} - {3^2} = 27\) nên \(BI = \sqrt {27} \approx 5,2cm\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}IC.AB \approx \frac{1}{2}.5,2.6 = 15,6\left( {c{m^2}} \right)\)
Thể tích hình chóp là: \(V = \frac{1}{3}.15,6.8 = 41,6\left( {c{m^3}} \right)\)
