
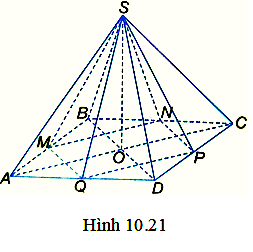
Cho hình chóp tứ giác đều S.ABCD có thể tích bằng \(144c{m^3}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (H.10.21)
Tính thể tích của hình chóp S.MNPQ.

Sử dụng kiến thức về thể tích của hình chóp tứ giác đều: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.

Advertisements (Quảng cáo)
Gọi O là giao điểm của AC và BD.
MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}AC\)
MQ là đường trung bình của tam giác ABD nên \(MQ = \frac{1}{2}BD\)
Diện tích hình vuông MNPQ là:
\({S_{MNPQ}} = \frac{1}{2}MN.MQ = \frac{1}{2}.AC.\frac{1}{2}BD = \frac{1}{2}\left( {\frac{1}{2}AC.BD} \right) = \frac{1}{2}{S_{ABCD}}\)
Hai hình chóp S.ABCD và S.MNPQ có chung chiều cao SO và \({S_{MNPQ}} = \frac{1}{2}{S_{ABCD}}\) nên \({V_{S.MNPQ}} = \frac{1}{2}{V_{S.ABCD}} = \frac{1}{2}.144 = 72\left( {c{m^3}} \right)\)
