
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:
a) \(EF = AH\)
b) \(AM \bot EF\)

a) Chứng minh tứ giác AFHE là hình chữ nhật dựa vào dấu hiệu: tứ giác có ba góc vuông là hình chữ nhật, từ đó suy ra \(EF = AH\)
b) Chứng minh \(\widehat {MAB} + \widehat {DEA} = {90^0}\) để suy ra \(AM \bot EF\)

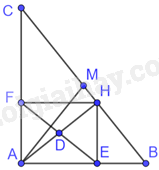
a) Vì tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên \(HE \bot AB,HF \bot AC\)
Do đó, \(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = {90^0}\)
Advertisements (Quảng cáo)
Tứ giác AFHE có: \(\widehat {BAC} = \widehat {HEA} = \widehat {HFA} = {90^0}\) nên tứ giác AFHE là hình chữ nhật. Do đó, \(AH = FE\)
b) Vì tứ giác AFHE là hình chữ nhật nên \(\widehat {FHE} = {90^0}\)
Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên \(AM = MB = MC = \frac{1}{2}BC\)
Tam giác AMB có: \(AM = MB\) nên tam giác AMB cân tại M. Do đó, \(\widehat {MAB} = \widehat B\)
Lại có: \(\widehat B = \widehat {DHE}\left( { = {{90}^0} - \widehat {HEB}} \right)\) nên \(\widehat {MAB} = \widehat {DHE}\) (1)
Gọi D là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE. Do đó, \(DH = DE = DF = DA\)
Tam giác DAE có: \(DA = DE\) nên tam giác DAE cân tại D, suy ra \(\widehat {DAE} = \widehat {DEA}\)
Mà AE//FH (do AFHE là hình chữ nhật) nên \(\widehat {DHF} = \widehat {DAE}\) (so le trong)
Do đó, \(\widehat {DEA} = \widehat {DHF}\) (2)
Lại có: \(\widehat {DHF} + \widehat {DHE} = \widehat {FHE} = {90^0}\) (3)
Từ (1), (2), (3) ta có: \(\widehat {MAB} + \widehat {DEA} = {90^0}\). Suy ra: \(AM \bot EF\)
