Giả sử ABCD là hình chữ nhật. Gọi E, H, G, F lần lượt là trung điểm của các cạnh AB; AD; DC; CB. Giải và trình bày phương pháp giải bài 3.31 trang 72 SGK Toán 8 tập 1 - Kết nối tri thức Bài 14. Hình thoi và hình vuông. Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi...

Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

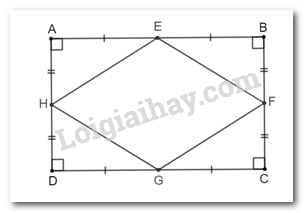
Giả sử ABCD là hình chữ nhật. Gọi E, H, G, F lần lượt là trung điểm của các cạnh AB; AD; DC; CB.
Chứng minh các cạnh bằng nhau suy ra EFGH là hình thoi

Advertisements (Quảng cáo)
Xét các tam giác AEH, BEF, CGF, DGH có:
\( \widehat A = \widehat B = \widehat C = \widehat D = 90^0\)
AE = BE = CG = DG (vì E, G là trung điểm của AB, CD và AB = CD)
BF = FC = DH = HA (vì F, H là trung điểm của BC, AD và BC = AD)
\( \Rightarrow \Delta AEH = \Delta BEF = \Delta CGF = \Delta DGH \)
Suy ra EH = EF = FG = GH (các cạnh tương ứng) nên tứ giác EFGH là hình thoi (vì có 4 cạnh bằng nhau).
