
Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.56).

Kẻ IM, dựa vào tính chất của đường trung tuyến ứng với cạnh huyền, ta có \(AB = MI = \frac{{A{\rm{D}}}}{2}\).
Tính các cạnh của hình chữ nhật dựa vào công thức tính chu vi hình chữ nhật.

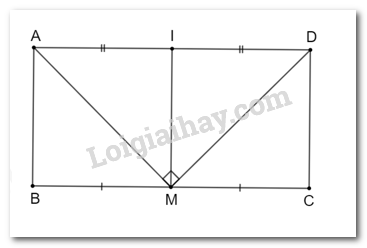
Gọi I là trung điểm của AD.
Theo tính chất của đường trung tuyến ứng với cạnh huyền, ta có \(MI = \frac{{A{\rm{D}}}}{2}\). (1)
Advertisements (Quảng cáo)
Xét tứ giác ABMI có: \( \widehat A = \widehat B = \widehat I = 90^0 \Leftrightarrow ABMI\) là hình chữ nhật.
=> AB = MI. (2)
Từ (1) và (2) suy ra \(AB = \frac{{A{\rm{D}}}}{2}\) nên AD = 2AB.
Mà \(AB + A{\rm{D}} = \frac{{36}}{2} = 18\) (cm).
Suy ra AB + 2AB = 18
Hay 3AB = 18
Do đó AB = 6 (cm).
Suy ra AD = 2AB = 2 . 6 = 12 (cm).
Vậy độ dài các cạnh của hình chữ nhật ABCD là AB = CD = 6 cm; AD = BC = 12 cm.
