Câu hỏi/bài tập:

Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.39.
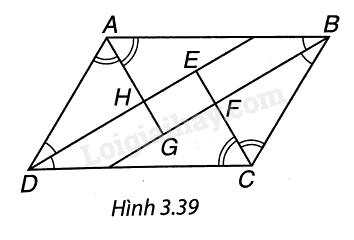
Chứng minh rằng EFGH là hình chữ nhật.

Chứng minh ba góc của tứ giác EFGH là góc vuông.
Advertisements (Quảng cáo)

Ta sẽ chứng minh ba góc của tứ giác EFGH là góc vuông.
Xét tam giác ECD có: \(\widehat {ECD} = \frac{1}{2}\widehat {BCD}\) (do EC là đường phân giác của \(\widehat {BCD}\)),
\(\widehat {EDC} = \frac{1}{2}\widehat {ADB}\) (do ED là đường phân giác của \(\widehat {ADB}\)), mà \(\widehat {BCD} + \widehat {ADC} = 180^\circ \) nên \(\widehat {ECD} + \widehat {EDC} = 90^\circ \).
Từ đó, tam giác ECD vuông tại E.
Tương tự, chứng minh được tam giác FBC vuông tại F, tam giác AHD vuông tại H. Tứ giác EFGH có ba góc vuông nên là hình chữ nhật.
