Câu hỏi/bài tập:

Cho hình chữ nhật ABCD. Gọi O là trung điểm của AC. Hạ OM vuông góc với BC tại M, ON vuông góc với BC tại N.
a) Chứng minh \(OA = \frac{1}{2}BD.\)
b) Chứng minh MN = OC.
c) Kẻ BK vuông góc với AC tại K, OM giao với BK tại H. Chứng minh CH vuông góc với MB.

a) Dựa vào tính chất của hình chữ nhật: Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Advertisements (Quảng cáo)
b) Chứng minh OMCN là hình chữ nhật suy ra MN = OC.
c) Chứng minh H là trực tâm tam giác OBC suy ra CH vuông góc với OB. (đề bài trong vở thực hành sai)

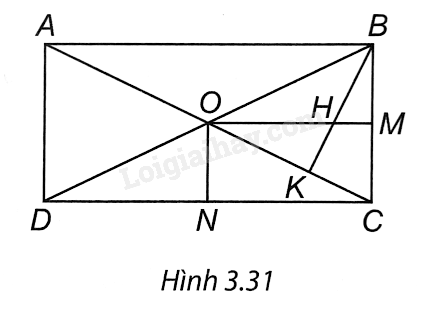
(H.3.31). a) Vì ABCD là hình chữ nhật nên AC cắt BD tại O và OA = OB = OD.
⇒ \(OA = OB = \frac{1}{2}BD.\)
b) Tứ giác OMCN có \(\hat M = \hat N = \hat C = 90^\circ \) nên OMCN là hình chữ nhật ⇒ MN = OC.
c) Trong tam giác BOC có OM, BK là đường cao cắt nhau tại H nên H là trực tâm ⇒ CH ⊥ OB.
