Câu hỏi/bài tập:

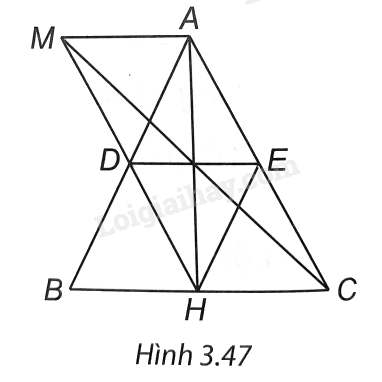
Cho tam giác ABC cân tại A. Gọi H là chân đường cao hạ từ A, D và E lần lượt là trung điểm của AB, AC. Lấy M là điểm trên DH sao cho MD = DH. Chứng minh rằng:
a) Tứ giác ADHE là hình thoi.
b) Tứ giác AHBM là hình chữ nhật.
c) Tứ giác ACHM là hình bình hành.
d) Ba đường thẳng MC, DE, AH đồng quy.

Dựa vào dấu hiệu nhận biết của các hình đã học.
Sử dụng tính chất các hình đã học để chứng minh ba điểm đồng quy.

Advertisements (Quảng cáo)
(H.3.47). a) Ta có AE = EC, CH = HB ⇒ HE là đường trung bình của ∆CAB.
⇒ HE // AC, HE = \(\frac{1}{2}\)AC = AD.
⇒ Tứ giác ADHE là hình bình hành.
∆ABC cân tại A nên AB = AC.
⇒ AE = \(\frac{1}{2}\)AC = \(\frac{1}{2}\)AB = AD.
Vậy hình bình hành ADHE có hai cạnh kề nhau bằng nhau nên là hình thoi.
b) Ta có MD = DH, DA = AB nên tứ giác AHBM có hai đường chéo AB và MH cắt nhau tại trung điểm mỗi đường nên là hình bình hành, hơn nữa \(\widehat {AHC} = 90^\circ \), suy ra AHBM là hình chữ nhật.
c) Tứ giác AHBM là hình chữ nhật nên AM // BH, AM = BH.
∆ABC cân tại A, AH ⊥ BC nên BH = CH.
Tứ giác ACHM có AM // CH, AM = CH nên là hình bình hành.
d) Tứ giác ACHM là hình bình hành nên MC, AH cắt nhau tại trung điểm mỗi đường. Tứ giác ADHE là hình thoi nên AH, DE cắt nhau tại trung điểm mỗi đường.
Vậy MC, DE, AH cắt nhau tại cùng một điểm nên chúng đồng quy.
