Hoạt động (HĐ) 1
Gợi ý giải câu hỏi Hoạt động 1 trang 75 SGK Toán 9
Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
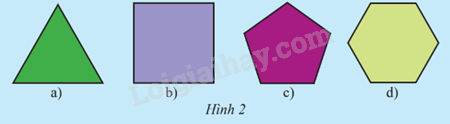

Nhìn hình nhận xét.

- Độ dài các cạnh của mỗi đa giác là bằng nhau.
- Số đo góc của mỗi đa giác là bằng nhau.
Thực hành (TH) 1
Hướng dẫn giải câu hỏi Thực hành 1 trang 77 SGK Toán 9
Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung \(\overset\frown{MN},\overset\frown{NP},\overset\frown{PQ},\overset\frown{QR},\overset\frown{RM}\) bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao?

- Đọc kĩ dữ kiện đề bài để vẽ hình
- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.

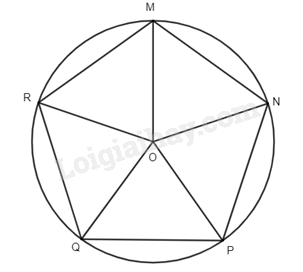
Các cung \(\overset\frown{MN}, \overset\frown{NP}, \overset\frown{PQ}, \overset\frown{QR}, \overset\frown{RM}\) chia đường tròn (O; R) thành 6 cung có số đo bằng nhau, suy ra số đo mỗi cung là 360o : 5 = 72o.
Ta có \(\widehat {MON}\) là góc nội tiếp chắn cung MN suy ra \(\widehat {MON}\) = 72o .
Xét \(\Delta \)MON, có: OM = ON = R suy ra \(\Delta \) MON cân tại O.
Suy ra \(\widehat {OMN} = \widehat {ONM}\) (tính chất tam giác cân)
Suy ra \(\widehat {OMN} = \widehat {ONM} = \frac{{{{180}^o} - \widehat {MON}}}{2} = {54^o}\).
Tương tự, ta có \(\widehat {OPN} = \widehat {ONP} = {54^o}\).
Suy ra \(\widehat {MPN} = \widehat {ONM} + \widehat {ONP} = {54^o} + {54^o} = {108^o}\).
Xét \(\Delta \) OMN và \(\Delta \) ONP có:
\(\widehat {MON} = \widehat {NOP}\);
OM = OP;
ON chung.
Suy ra \(\Delta \) OMN = \(\Delta \) ONP (c – g – c).
Do đó, MN = NP (hai cạnh tương ứng).
Chứng minh tương tự ta thu được ngũ giác MNPQR có các cạnh bằng nhau và các góc đều bằng nhau ( = 108o).
Vậy MNPQR là một đa giác đều.
Vận dụng (VD) 1
Advertisements (Quảng cáo)
Hướng dẫn giải câu hỏi Vận dụng 1 trang 77 SGK Toán 9
Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?

- Đọc kĩ dữ kiện đề bài để vẽ hình
- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.

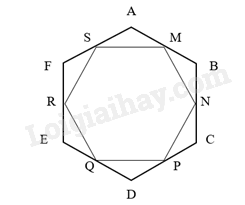
Do ABCDEF là lục giác đều nên:
\(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = \widehat F = {120^o}\).
- AB = BC = CD = DE = EF = FA.
Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA.
Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.
Xét \(\Delta \) SAM và \(\Delta \) MBN có:
\(\widehat A = \widehat B\) (chứng minh trên);
AM = BN (chứng minh trên);
SA = MB (chứng minh trên).
Suy ra \(\Delta \) SAM = \(\Delta \) MBN (c – g – c).
Do đó, SM = MN (hai cạnh tương ứng).
Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM (1).
Vì AS = AM (chứng minh trên) suy ra \(\Delta \) ASM cân tại A.
suy ra \(\widehat {ASM} = \widehat {AMS}\) (tính chất tam giác cân)
Nên \(\widehat {ASM} = \widehat {AMS} = \frac{{{{180}^o} - \widehat A}}{2} = {30^o}\) (tổng 3 góc trong của tam giác).
Tương tự ta thu được:
\(\widehat {BMN} = \widehat {BNM} = \frac{{{{180}^o} - \widehat B}}{2} = 30\);
\(\widehat {CNP} = \widehat {CPN} = \frac{{{{180}^o} - \widehat C}}{2} = {30^o}\);
\(\widehat {DPQ} = \widehat {DQP} = \frac{{{{180}^o} - \widehat D}}{2} = {30^o}\);
\(\widehat {EQR} = \widehat {ERQ} = \frac{{{{180}^o} - \widehat E}}{2} = {30^o}\);.
\(\widehat {FRS} = \widehat {FSR} = \frac{{{{180}^o} - \widehat F}}{2} = {30^o}\)
Ta có:
\(\widehat {RSM} = {180^o} - \widehat {FRS} - \widehat {ASM} = {180^o} - {30^o} - {30^o} = {120^o}\)
Tương tự, ta được:
\(\widehat {AMN} = \widehat {MNP} = \widehat {NQP} = \widehat {PQR} = \widehat {QRS} = {120^o}\). (2)
Từ (1) và (2), suy ra MNPQRS là đa giác đều.
