
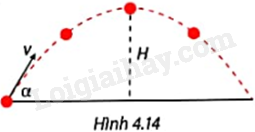
Khi một vật được ném xiên một góc \(\alpha \) so với mặt đất và tốc độ ném ban đầu là \({v_o}\left( {m/s} \right)\) (Hình 4.14), độ cao lớn nhất H(m) mà vật có thể đạt đến được cho bởi công thức: \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) (nguồn: https://phys.libretexts.org/Bookshelves/University_Physics/Physics_(Boundless)/3%3A_Two-Dimensional_Kinematics/3.3%3A_Projectile_Motion). Tính độ cao lớn nhất của vật nếu tốc độ ném ban đầu là 12m/s và góc ném là:
a) \({45^o}\);
b) \({30^o}\);
c) \({50^o}\).
Làm tròn kết quả đến hàng phần mười mét.

a) Thay \({v_o} = 12,\alpha = {45^o}\) vào công thức \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) để tính chiều cao H.
Advertisements (Quảng cáo)
b) Thay \({v_o} = 12,\alpha = {30^o}\) vào công thức \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) để tính chiều cao H.
c) Thay \({v_o} = 12,\alpha = {50^o}\) vào công thức \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) để tính chiều cao H.

a) Thay \({v_o} = 12,\alpha = {45^o}\) vào công thức \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) ta có:
\(H = \frac{1}{{20}}{.12^2}{\left( {\sin {{45}^o}} \right)^2} = \frac{{18}}{5}\left( m \right)\).
b) Thay \({v_o} = 12,\alpha = {30^o}\) vào công thức \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) ta có:
\(H = \frac{1}{{20}}{.12^2}{\left( {\sin {{30}^o}} \right)^2} = \frac{9}{5}\left( m \right)\).
c) Thay \({v_o} = 12,\alpha = {50^o}\) vào công thức \(H = \frac{1}{{20}}v_o^2{\left( {\sin \alpha } \right)^2}\) ta có:
\(H = \frac{1}{{20}}{.12^2}{\left( {\sin {{50}^o}} \right)^2} \approx 4,2\left( m \right)\).
