
Trên mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Xác định:
a) Vị trí tương đối của đường tròn tâm M, bán kính 3 với hai trục Ox và Oy;
b) Bán kính của đường tròn tâm M tiếp xúc với trục Ox.

Cho đường tròn (O; R) và đường thẳng a. Đặt d là khoảng cách từ O đến đường thẳng a. Vị trí tương đối của đường thẳng a và đường tròn (O; R) có thể được xác định dựa vào mối quan hệ giữa R và d như sau:
+ Nếu \(d > R\) thì đường thẳng a và đường tròn (O) không giao nhau.
Advertisements (Quảng cáo)
+ Nếu \(d = R\) thì đường thẳng a và đường tròn (O) tiếp xúc nhau.
+ Nếu \(d < R\) thì đường thẳng a và đường tròn (O) cắt nhau.

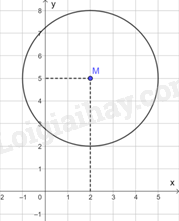
a) Khoảng cách từ M đến trục Oy bằng 2. Vì \(2 < 3\) nên đường tròn tâm M, bán kính 3 cắt trục Oy.
Khoảng cách từ M đến trục Ox bằng 5. Vì \(5 > 3\) nên đường tròn tâm M, bán kính 3 và trục Ox không giao nhau.
b) Để đường tròn tâm M tiếp xúc với trục Ox thì bán kính đường tròn tâm M bằng khoảng cách từ M đến trục Ox. Do đó, bán kính đường tròn tâm M bằng 5.
