
Cho điểm A thuộc đường tròn (O). Trên tiếp tuyến tại A của (O) xác định điểm M sao cho \(AM = AO\). Đường thẳng OM cắt (O) tại B và C (B nằm giữa O và M).
a) Tính góc ở tâm BOA.
b) Tính số đo cung lớn AC.

a) Chứng minh tam giác MOA vuông cân tại O, suy ra \(\widehat {BOA} = {45^o}\).
b) Tính số đo góc AOC, từ đó tính số đo cung AC nhỏ, từ đó tính được số đo cung AC lớn.
Advertisements (Quảng cáo)

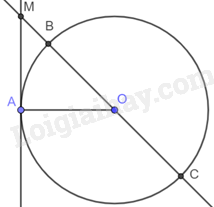
a) Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\), suy ra tam giác AMO vuông tại A. Mà \(MA = OA\) nên tam giác AMO vuông cân tại O. Do đó, \(\widehat {BOA} = {45^o}\).
b) Ta có: \(\widehat {AOC} = {180^o} - \widehat {BOA} = {135^o}\)
Vì AOC là góc ở tâm chắn cung nhỏ AC nên \(sđ\overset\frown{A{{C}_{nhỏ}}}={{135}^{o}}\).
Số đo cung AC lớn là: \({360^o} - {135^o} = {225^o}\).
