
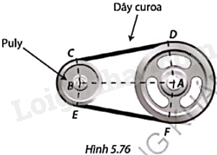
Trong Hình 5.76, hai puly có dạng hình tròn tâm A bán kính 12,5cm và tâm B bán kính 7cm được nối bằng dây curoa. Khoảng cách giữa tâm của hai puly là \(AB = 30cm\). Đoạn dây CD, EF tiếp xúc với cả hai puly. Tính:
a) Độ dài CD và số đo các góc của tứ giác ABCD;
b) Độ dài dây curoa.
Làm tròn độ dài đến hàng phần mười centimét, số đo góc đến phút.

a) + Kẻ BG vuông góc với AD tại G.
+ Chứng minh tứ giác BCDG là hình chữ nhật suy ra \(CD = BG\), \(BC = DG\)
+ Áp dụng định lí Pythagore vào tam giác ABG vuông tại G để tính BG, AG; tính cos GAB, từ đó tính góc GAB.
+ Tứ giác ABCD có: \(\widehat C + \widehat D + \widehat {DAB} + \widehat {ABC} = {360^o}\), từ đó tính được góc ABC.
b) + Tính số đo cung lớn FD, số đo cung nhỏ CE.
+ Tính độ dài cung lớn FD, độ dài cung nhỏ CE.
+ Độ dài dây curoa là: \({l_{DF}} + {l_{CE}} + CD + EF\).

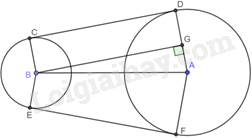
Kẻ BG vuông góc với AD tại G. Suy ra: \(\widehat {BGD} = \widehat {BGA} = {90^o}\).
Vì CD là tiếp tuyến của hai đường tròn (B) và (A) nên \(BC \bot CD,CD \bot AD\) nên \(\widehat {BCD} = \widehat {CDG} = {90^o}\).
Tứ giác BGDC có: \(\widehat {BCD} = \widehat {CDG} = \widehat {BGD} = {90^o}\) nên tứ giác BGDC là hình chữ nhật.
Do đó, \(CD = BG\), \(BC = DG = 7cm\).
Tam giác BGA vuông tại G nên:
Advertisements (Quảng cáo)
+ \(\cos GAB = \frac{{GA}}{{AB}} = \frac{{DA - GD}}{{AB}} = \frac{{5,5}}{{30}} = \frac{{11}}{{60}}\) nên \(\widehat {GAB} \approx {79^o}26’\)
+ \(B{G^2} + G{A^2} = A{B^2}\),
\(BG = \sqrt {A{B^2} - {{\left( {AD - DG} \right)}^2}} = \sqrt {{{30}^2} - {{\left( {12,5 - 7} \right)}^2}} = \frac{{7\sqrt {71} }}{2}\left( {cm} \right)\)
nên \(CD = \frac{{7\sqrt {71} }}{2}cm\)
Chứng minh tương tự ta có: \(EF = \frac{{7\sqrt {71} }}{2}cm\)
Tứ giác ABCD có: \(\widehat C + \widehat D + \widehat {DAB} + \widehat {ABC} = {360^o}\)
\(\widehat {ABC} = {360^o} - \left( {\widehat C + \widehat D + \widehat {DAB}} \right) \approx {360^o} - \left( {{{90}^o} + {{90}^o} + {{79}^o}26′} \right) \approx {100^o}34’\)
b) Chứng minh tương tự phần a ta có:
\(\widehat {FAB} \approx {79^o}26’\), \(\widehat {EBF} \approx {100^o}34’\)
Do đó, \(\widehat {DAF} = \widehat {DAB} + \widehat {FAB} \approx {158^o}52’\).
Do đó, số đo cung nhỏ DF là: \({158^o}52’\).
Suy ra, số đo cung lớn DF là:
\({360^o} - {158^o}52′ = {201^o}8’\)
Số đo cung CE nhỏ là: \({158^o}52’\).
Độ dài cung lớn DF là:
\({l_{DF}} = \frac{{\pi {{.12.201}^o}8′}}{{{{180}^o}}} = \frac{{3017\pi }}{{225}}\left( {cm} \right)\)
Độ dài cung nhỏ CE là:
\({l_{CE}} = \frac{{\pi .7,{{5.158}^o}52′}}{{180}} = \frac{{2383\pi }}{{360}}\left( {cm} \right)\)
Độ dài dây curoa là:
\({l_{DF}} + {l_{CE}} + CD + EF \approx \frac{{3017\pi }}{{225}} + \frac{{2383\pi }}{{360}} + 2.\frac{{7\sqrt {71} }}{2} \approx 121,9\left( {cm} \right)\)
