
Trong Hình 5.77, mỗi làn chạy của sân vận động được thiết kế gồm hai phần là đường chạy thẳng và hai phần có dạng nửa đường tròn. Trong một cuộc thi điền kinh, vận động viên ở làn trong cùng xuất phát từ vị trí điểm A, chạy ngược chiều kim đồng hồ đúng một vòng và về đích ở điểm A.
a) Tính cự li chạy của cuộc thi (tổng quãng đường vận động viên phải chạy).
b) Để đảm bảo cự li chạy như nhau, vận động viên ở làn ngoài cùng không chạy đúng một vòng mà xuất phát từ vị trí điểm B và về đích ở điểm C. Xác định số đo góc COB.
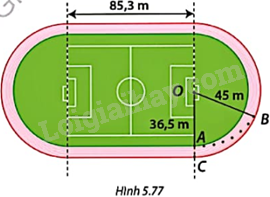

a) Tổng quãng đường vận động viên phải chạy bằng tổng độ dài 2 đường chạy thẳng dài, mỗi đường dài 85,3m và hai phần có dạng nửa đường tròn có bán kính 36,5m.
b) + Độ dài cung CB bằng độ dài làn ngoài cùng – tổng cự li chạy của cuộc thi.
+ Áp dụng công thức tính độ dài cung CB, để tính số đo cung CB nhỏ, từ đó tính được góc COB.

Advertisements (Quảng cáo)
a) Độ dài hai nửa đường tròn bán kính 36,5m là:
\({C_1} = 2.\pi .36,5 = 73\pi \left( m \right)\)
Tổng cự li chạy của cuộc là:
\(C = 73\pi + 85,3.2 = 73\pi + 170,6\left( m \right)\)
b) Độ dài làn ngoài cùng là:
\({C_2} = 2\pi .45 + 85,3.2 = 90\pi + 170,6\left( m \right)\)
Độ dài cung CB là:
\({C_3} = {C_2} - {C_1} = 90\pi + 170,6 - 73\pi - 170,6 = 17\pi \left( {cm} \right)\)
Do đó, $17\pi =\frac{\pi .45.sđ\overset\frown{BC}}{180}$, suy ra: $sđ\overset\frown{BC}={{68}^{o}}$
Vì BOC là góc ở tâm chắn cung BC nhỏ nên $\widehat{BOC}=sđ\overset\frown{BC}={{68}^{o}}$
