
Cho MA và MB là hai tiếp tuyến của đường tròn (O; R) (A, B là hai tiếp điểm) sao cho \(\Delta \)MAB là tam giác đều. Khoảng cách OM bằng
A. \(\frac{1}{2}R\).
B. R.
C. 2R.
D. \(R\sqrt 2 \).

+ Chứng minh \(\widehat {AMB} = {60^o}\).
+ Chứng minh MO là tia phân giác \(\widehat {AMB}\), nên \(\widehat {AMO} = \frac{1}{2}\widehat {AMB}\).
Advertisements (Quảng cáo)
+ Chứng minh tam giác AOM vuông tại M nên \(AO = MO.\sin AMO\), từ đó tính được MO.

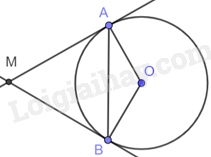
Vì tam giác MAB đều nên \(\widehat {AMB} = {60^o}\).
Vì MA và MB là tiếp tuyến của (O) nên MO là tia phân giác \(\widehat {AMB}\), nên \(\widehat {AMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.60^o} = {30^o}\)
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác MAO vuông tại A.
Suy ra, \(AO = MO.\sin AMO\) nên
\(MO = \frac{{AO}}{{\sin AMO}} = \frac{R}{{\sin {{30}^o}}} = 2R\).
Chọn C
