Câu hỏi/bài tập:

Từ một tấm bìa hình chữ nhật với đồ dài hai cạnh là 20 cm, 15 cm có thể cuộn lại và dùng băng dính dán thành hình trụ A hoặc hình trụ B (không có nắp) như Hình 9.13.
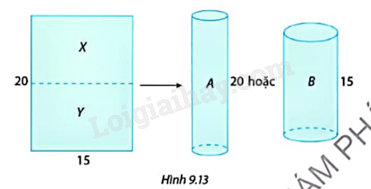
a) Hãy so sánh thể tích của hai hình trụ A và B. Giải thích câu trả lời của em.
b) Nếu cắt tấm bìa thành hai phần X, Y bằng nhau và tạo thành hai hình trụ (không có nắp) cùng chiều cao 15 cm thì tổng thể tích của hai hình trụ này có lớn hơn thể tích của hình trụ B không? Vì sao?

Dựa vào chu vi đường tròn C = \(2\pi r\) (với r là bán kính đường tròn).
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ).

a) Ta có chu vi đường tròn đáy hình trụ A là:
\(2\pi r = 15\)suy ra r = \(\frac{{15}}{{2\pi }}\) cm
Thể tích hình trụ A là:
Advertisements (Quảng cáo)
\({V_A} = \pi {r^2}h = \pi .{\left( {\frac{{15}}{{2\pi }}} \right)^2}.20 = \frac{{1125}}{\pi }\) cm3
Ta có chu vi đường tròn đáy hình trụ B là:
\(2\pi r = 20\)suy ra r = \(\frac{{20}}{{2\pi }} = \frac{{10}}{\pi }\) cm
Thể tích hình trụ B là:
\({V_B} = \pi {r^2}h = \pi .{\left( {\frac{{10}}{\pi }} \right)^2}.15 = \frac{{1500}}{\pi }\) cm3
Vậy thể tích hình trụ B lớn hơn thể tích hình trụ A.
b) Ta có chu vi đường tròn đáy hình trụ chiều cao 15 cm là:
\(2\pi r = 10\)suy ra r = \(\frac{5}{\pi }\) cm
Thể tích hình trụ chiều cao 15 cm là:
\(\pi {r^2}h = \pi .{\left( {\frac{5}{\pi }} \right)^2}.15 = \frac{{375}}{\pi }\) cm3
Suy ra thể tích hai hình trụ chiều cao 15 cm là:
2. \(\frac{{375}}{\pi }\) = \(\frac{{750}}{\pi }\) cm3
Vậy tổng thể tích của hai hình trụ chiều cao 15 cm nhỏ hơn thể tích của hình trụ B.
