Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 111
Trong Hình 5.30, đường thẳng a tiếp xúc với đường tròn (O; R) tại A và H là chân đường vuông góc kẻ từ O xuống a. Xác định độ dài OH. Vì sao A và H trùng nhau, nhận xét về góc tạo bởi tiếp tuyến a và bán kính OA.
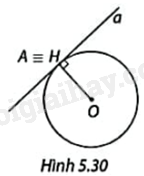

+ Chứng minh OH là khoảng cách từ O đến đường thẳng a. Mà đường thẳng a tiếp xúc với đường tròn (O; R) nên \(OH = R\).
+ Chứng minh \(OA = R\) và \(OA \bot a\) tại A, từ đó suy ra A và H trùng nhau.
+ Góc tạo bởi tiếp tuyến a và bán kính OA bằng \({90^o}\).

Vì H là chân đường vuông góc kẻ từ O xuống a nên OH là khoảng cách từ O đến đường thẳng a.
Mà đường thẳng a tiếp xúc với đường tròn (O; R) nên \(OH = R\).
Vì đường thẳng a tiếp xúc với đường tròn (O; R) tại A nên khoảng cách từ O đến đường thẳng a bằng bán kính đường tròn (O; R). Tức là: \(OA = R\) và \(OA \bot a\) tại A.
Do đó, A và H trùng nhau.
Góc tạo bởi tiếp tuyến a và bán kính OA bằng \({90^o}\).
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 111
Trong Hình 5.32, MN là tiếp tuyến của đường tròn (O; R) tại N. Tính R.
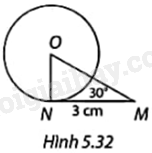

Chứng minh tam giác ONM vuông tại N, suy ra \(ON = NM.\tan M\)

Vì MN là tiếp tuyến của đường tròn (O; R) tại N nên \(ON \bot MN\). Do đó, tam giác ONM vuông tại N.
Suy ra \(ON = NM.\tan M = 3.\tan {30^o} = \sqrt 3 \)
Hoạt động2
Advertisements (Quảng cáo)
Trả lời câu hỏi Hoạt động 2 trang 112
Trong Hình 5.33, đường tròn (O) có bán kính R và điểm A nằm trên đường tròn, đường thẳng a vuông góc với OA tại A. So sánh khoảng cách từ O đến đường thẳng a với bán kính R, từ đó xác định vị trí tương đối của a và (O).
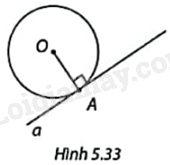

+ Chỉ ra \(OA = R\).
+ Chứng minh khoảng cách từ O đến đường thẳng a là: \(OA = R\).
+ Suy ra, đường thẳng a tiếp xúc với (O).

Vì A nằm trên đường tròn (O) nên \(OA = R\).
Vì đường thẳng a vuông góc với OA tại A nên khoảng cách từ O đến đường thẳng a là: \(OA = R\).
Do đó, đường thẳng a tiếp xúc với (O).
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 112
Trong Hình 5.35, cạnh mỗi hình vuông trong lưới ô vuông có độ dài là 1 đơn vị. Chứng minh rằng đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
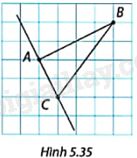

+ Sử dụng định lí Pythagore tính AB, BC, AC.
+ Sử dụng định lí Pythagore đảo chứng minh tam giác ABC vuông tại A, từ đó suy ra đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA

Ta có:
\(\begin{array}{l}A{B^2} = {2^2} + {4^2} = 20,\\B{C^2} = {3^2} + {4^2} = 25,\\A{C^2} = {1^2} + {2^2} = 5.\end{array}\)
Do đó, \(A{B^2} + A{C^2} = B{C^2}\) nên tam giác ABC vuông tại A. Suy ra, \(AB \bot AC\).
Suy ra, đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
