Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 115
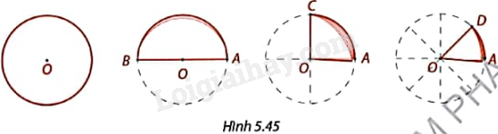
Cắt một hình tròn bằng giấy và gấp làm hai, làm tư, làm tám như trong Hình 5.45.
1. Cho biết giao điểm O của các đường gấp ở đâu trong hình tròn?
2. Các đường gấp chia hình tròn thành nhiều phần. Trong mỗi trường hợp, hãy:
a) Cho biết khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau không?
b) So sánh số đo các góc đỉnh O trong mỗi phần và tính tổng số đo các góc đỉnh O trong tất cả các phần

Quan sát hình đã gấp rồi rút ra kết luận.

1. Giao điểm O của các đường gấp là tâm của hình tròn.
2. a) Khi đường tròn (O) được gấp lại, các cung của đường tròn nằm trong các phần chồng khít lên nhau.
b) + Khi gấp hình tròn làm hai: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 180 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
Advertisements (Quảng cáo)
+ Khi gấp hình tròn làm tư: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 90 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
+ Khi gấp hình tròn làm tám: Số đo các góc ở đỉnh O trong mỗi phần bằng nhau và bằng 45 độ.
Tổng số đo của tất cả các góc đỉnh O đều bằng 360 độ.
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 117
Xác định số đo của các cung MxN, NyP và MzP trong Hình 5.48.
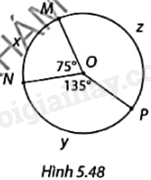

Số đo của cung nhỏ là số đo của góc ở tâm chắn cung đó.

Ta có: $\widehat{MOP}$ $={{360}^{o}}-\widehat{MON}-\widehat{NOP}$ $={{360}^{o}}-{{75}^{o}}-{{135}^{o}}$ $={{150}^{o}}$.
Góc MON là góc ở tâm chắn cung MxN nên $sđ\overset\frown{MxN}$ $=\widehat{MON}$ $={{75}^{o}}$.
Góc PON là góc ở tâm chắn cung NyP nên $sđ\overset\frown{NyP}$ $=\widehat{PON}$ $={{135}^{o}}$.
Góc MOP là góc ở tâm chắn cung MzP nên $sđ\overset\frown{MzP}$ $=\widehat{MOP}$ $={{150}^{o}}$.
