Gợi ý giải câu hỏi Thực hành trang 27
Dùng phần mềm Geogebra vẽ đồ thị của các hàm số sau và tìm toạ độ giao điểm (nếu có) của hai đồ thị:
1. \(y = \frac{1}{3}{{\rm{x}}^2}\) và \(y = - x + \frac{1}{2}\)
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \)
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\)
Bước 1. Vẽ đồ thị hàm số \(y = a{x^2}\).
Nhập lệnh y = ax^2.
Bước 2. Vẽ đồ thị hàm số y = ax + b.
Nhập lệnh y = ax + b.
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng 
để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
1. \(y = \frac{1}{3}{x^2}\) và \(y = - x + \frac{1}{2}\).
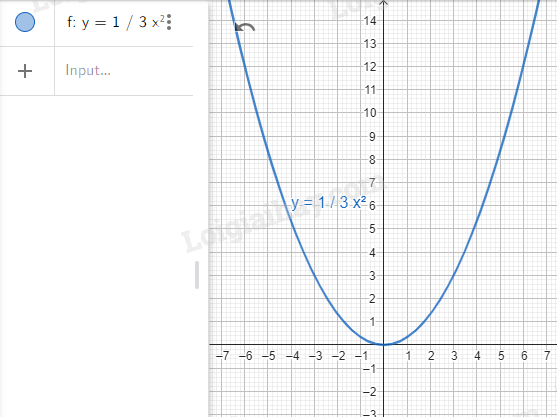
Bước 1. Vẽ đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Nhập lệnh y = 1/3*x^2
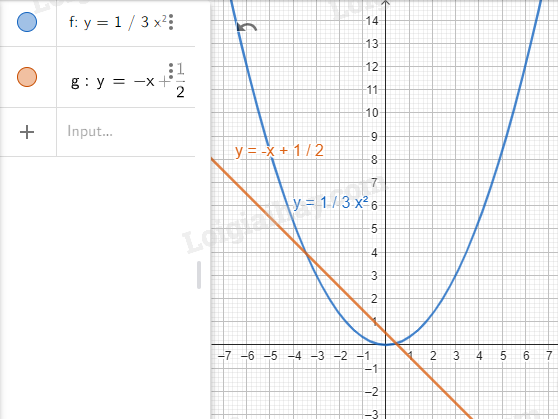
Bước 2. Vẽ đồ thị hàm số \(y = - x + \frac{1}{2}\).
Nhập lệnh y = -x + 1/2
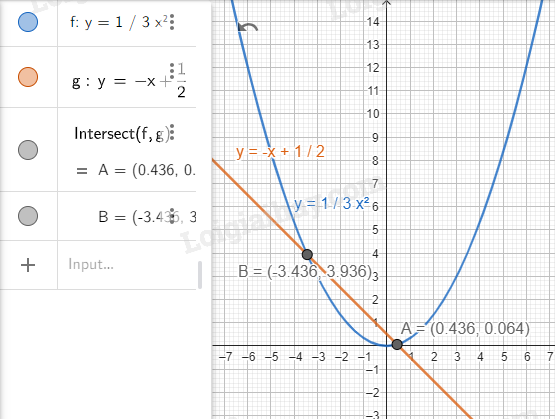
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l}\frac{1}{3}{x^2} = - x + \frac{1}{2}\\\frac{1}{3}{x^2} + x - \frac{1}{2} = 0\end{array}\)
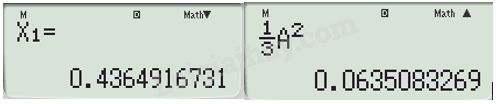
Ta được tọa độ điểm A.
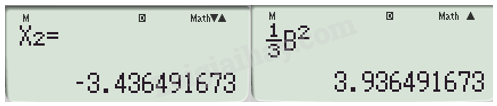
Ta được tọa độ điểm B.
2. \(y = \sqrt 2 {x^2}\) và \(y = 2x - \sqrt 3 \).
Advertisements (Quảng cáo)
Bước 1. Vẽ đồ thị hàm số \(y = \sqrt 2 {x^2}\).
Sử dụng bàn phím của GeoGebra để nhập kí hiệu \(\sqrt {...} \)
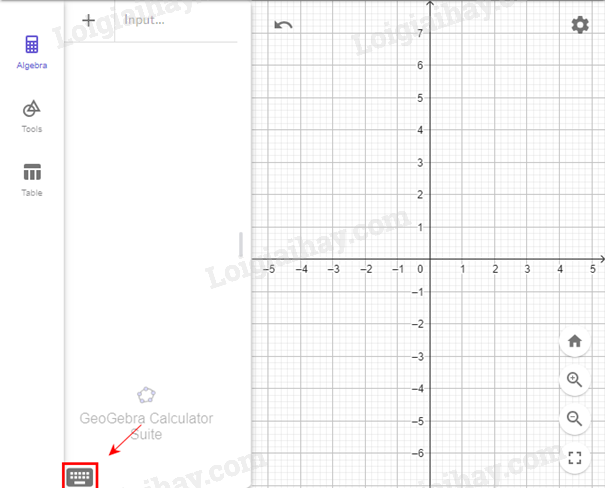
Ta được màn hình như sau:
Nhập lệnh: \(y = \sqrt 2 *x\^2\)
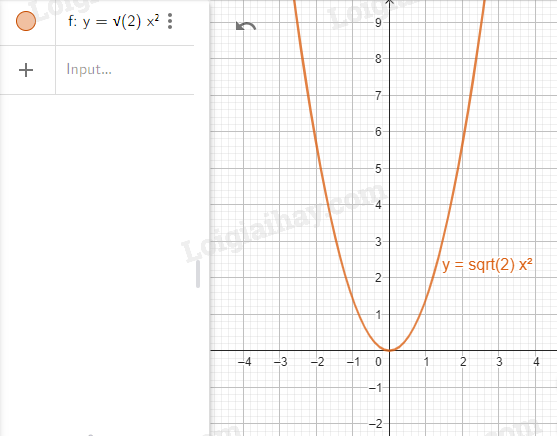
Bước 2. Vẽ đồ thị hàm số \(y = 2x - \sqrt 3 \).
Nhập lệnh \(y = 2x - \sqrt 3 \)
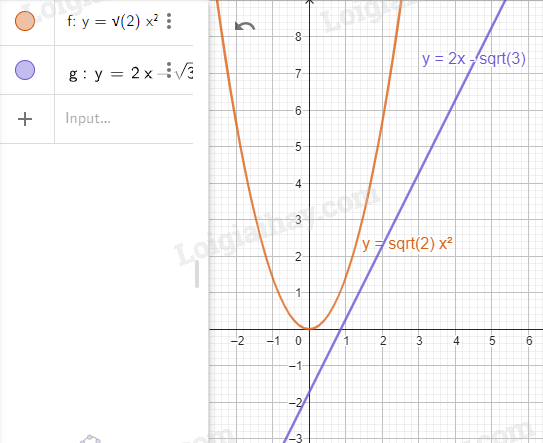
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng ta thấy hai đồ thị không có điểm chung.
Do đó không có giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l}\sqrt 2 {x^2} = 2x - \sqrt 3 \\\sqrt 2 {x^2} - 2x + \sqrt 3 = 0\end{array}\)
Sử dụng máy tính cầm tay để giải phương trình, ta được:
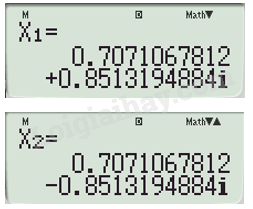
Vậy hai đồ thị không có giao điểm.
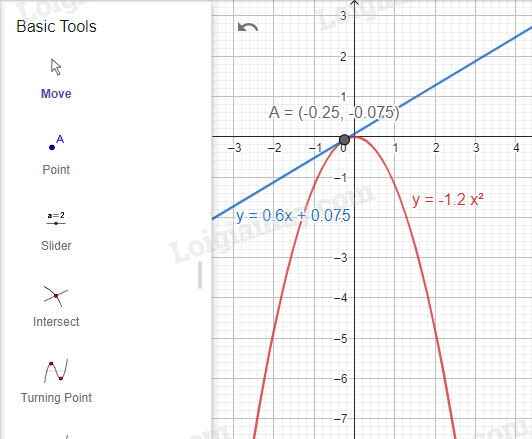
3. \(y = - 1,2{x^2}\) và \(y = 0,6x + 0,075\).
Bước 1. Vẽ đồ thị hàm số \(y = - 1,2{x^2}\).
Nhập lệnh y = -1.2*x^2
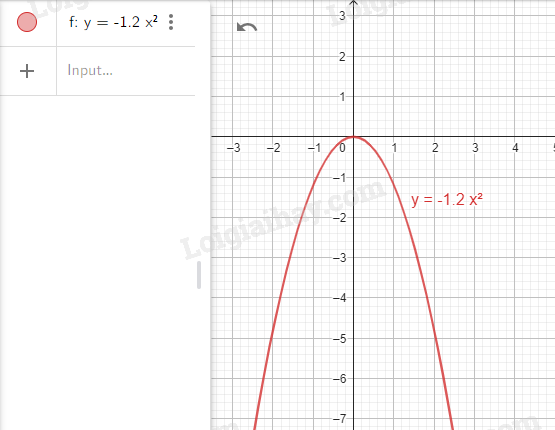
Bước 2. Vẽ đồ thị hàm số \(y = 0,6x + 0,075\).
Nhập lệnh \(y = 0.6x + 0.075\)
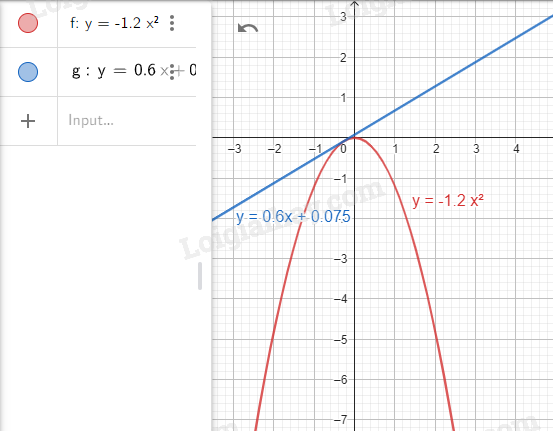
Bước 3. Tìm tọa độ giao điểm của hai đồ thị.
Dùng để tìm giao điểm của hai đồ thị.
Bước 4. Kiểm tra kết quả bằng cách sử dụng máy tính cầm tay giải phương trình bậc hai.
\(\begin{array}{l} - 1,2{x^2} = 0,6x + 0,075\\ - 1,2{x^2} - 0,6x - 0,075 = 0\end{array}\)
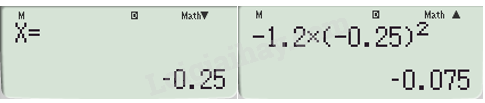
Ta được tọa độ điểm A.