Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 30
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC. (Hình 7.2)
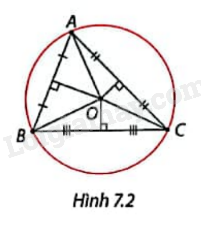

Ba đường trung trực của một tam giác cùng đi qua một điểm và điểm này cách đều ba đỉnh của tam giác.

Ta có ba đường trung trực của tam giác ABC cùng đi qua một điểm O nên ta có OC = OB = OA. Vì vậy đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC.
Luyện tập1
Advertisements (Quảng cáo)
Giải câu hỏi Luyện tập 1 trang 32
Tam giác đều ABC có cạnh bằng 4, M là trung điểm của BC và O là trọng tâm. Xác định tâm, bán kính và vẽ đường tròn ngoại tiếp tam giác ABC và AMC.

Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam đều có bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).

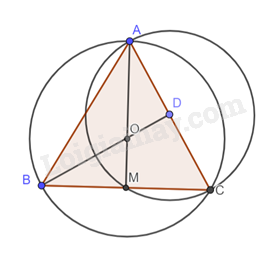
Đường tròn ngoại tiếp tam giác ABC có tâm là O, bán kính OA = \(\frac{{4\sqrt 3 }}{3}\) cm.
Đường tròn ngoại tiếp tam giác AMC có tâm là trung điểm AC là D, bán kính DA.
Ta có DA = \(\frac{1}{2}AC = \frac{1}{2}.4 = 2\) cm.
