Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 112
Vẽ đường tròn (O) và lấy hai điểm A, B thuộc (O) (AB không là đường kính). Vẽ tiếp tuyến tại A và B cắt nhau tại M. Em hãy đo và so sánh:
a) MA và MB;
b) \(\widehat {AMO}\) và \(\widehat {BMO}\);
c) \(\widehat {AOM}\) và \(\widehat {BOM}\).

Đo hình và đưa ra kết luận.

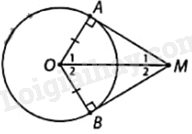
Tiến hành đo và so sánh ta có:
a) \(MA = MB\)
b) \(\widehat {AMO} = \widehat {BMO}\)
c) \(\widehat {AOM} = \widehat {BOM}\)
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 113
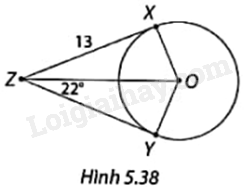
Trong Hình 5.38, ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Y. Xác định số đo \(\widehat {XOY}\) và độ dài YZ.

Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm;
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác góc tạo bởi hai bán kính đi qua các tiếp điểm.

ZX và ZY là hai tiếp tuyến của đường tròn tâm O với tiếp điểm lần lượt là X và Ynên
Advertisements (Quảng cáo)
+ \(YZ = ZX = 13\)
+ OZ là tia phân giác góc XOY nên \(\widehat {XOY} = 2\widehat {ZOY}\)
Vì ZY là tiếp tuyến của đường tròn tâm O nên \(ZY \bot OY\) nên tam giác ZOY vuông tại Y.
Do đó, \(\widehat {ZOY} = {90^o} - \widehat {YZO} = {90^o} - {22^o} = {68^o}\)
Vậy \(\widehat {XOY} = 2\widehat {ZOY} = {2.68^o} = {136^o}\).
Vận dụng
Trả lời câu hỏi Vận dụng trang 114
Trong Hình 5.39, người ta dùng một đoạn dây gắn vào hai điểm A, B trên viền một chiếc gương tròn để treo gương vào điểm M. Biết tổng độ dài dây là 82cm, \(\widehat {AMB} = {52^o}\) và MA, MB tiếp xúc với viền gương. Tính đường kính của gương. Làm tròn kết quả đến đơn vị centimét.
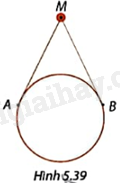

+ Vì MA, MB là tiếp tuyến của (O) nên \(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB}\) và \(MA = MB\).
+ Tam giác AMO vuông tại A nên \(OA = AM.\tan AMO\), từ đó tính được OA.
+ Đường kính của gương là: \(2OA\).

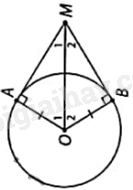
Gọi O là tâm của chiếc gương.
Vì MA, MB là tiếp tuyến của (O) nên:
+ MO là tia phân giác góc AMB, suy ra:
\(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.52^o} = {26^o}\).
+ \(MA = MB = \frac{{82}}{2} = 41cm\).
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác AMO vuông tại A.
Suy ra: \(OA = AM.\tan AMO = 41.\tan {26^o}\).
Vậy đường kính của gương là: \(2OA = 2.41.\tan {26^o} \approx 40\left( {cm} \right)\)
