Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 3
a) Cho hàm số \(y = \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.2
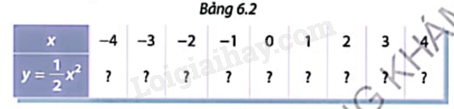
Đánh dấu các điểm (x;y) trong Bảng 6.2 trên mặt phẳng toạ độ.
b) Cho hàm số \(y = - \frac{1}{2}{x^2}.\) Tính các giá trị tương ứng của hàm số trong Bảng 6.3
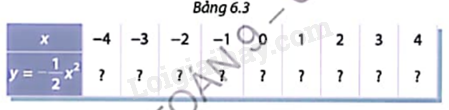

Thay lần lượt giá x vào hàm số \(y = \frac{1}{2}{x^2}\) và \(y = - \frac{1}{2}{x^2}\) để tính y.
Đánh dấu các điểm trên mặt phẳng toạ độ.

a)

Lấy các điểm A(-4;8), B(-3; \(\frac{9}{2}\)), C(-2;2), D(-1; \(\frac{1}{2}\)), O(0;0), A’(4;8), B’(3; \(\frac{9}{2}\)),
C’(2;2), D’(1; \(\frac{1}{2}\)) trên mặt phẳng toạ độ tạo một đường cong bên dưới.
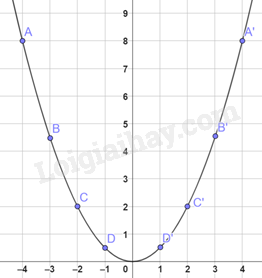
b)

Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 4
Quan sát đồ thị của hai hàm số \(y = \frac{1}{2}{x^2}\) (Hình 6.1a) và \(y = - \frac{1}{2}{x^2}\) (Hình 6.1b).
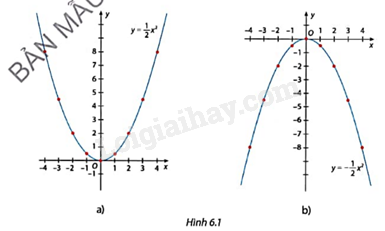
Với mỗi đồ thị, hãy đồ thị:
a) Đồ thị nằm phía trên hay phía dưới trục hoành;
b) Điểm thấp nhất hoặc điểm cao nhất của đồ thị;
c) Mối liên hệ giữa tung độ của hai điểm có hoành độ đối nhau thuộc đồ thị;
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy có trùng nhau hay không.

Nhìn vào đồ thị và nhận xét.

Với đồ thị \(y = \frac{1}{2}{x^2}\):
a) Đồ thị nằm phía trên trục hoành.
b) Điểm thấp nhất đồ thị là O(0;0)
c) Tung độ đối xứng với nhau qua trục Oy của hai điểm có hoành độ đối nhau thuộc đồ thị
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy trùng nhau.
Advertisements (Quảng cáo)
Với đồ thị \(y = - \frac{1}{2}{x^2}\):
a) Đồ thị nằm phía dưới trục hoành.
b) Điểm thấp cao đồ thị là O(0;0)
c) Tung độ đối xứng với nhau qua trục Oy của hai điểm có hoành độ đối nhau thuộc đồ thị
d) Nếu gấp giấy theo nếp gấp là đường thẳng chứa trục Oy thì phần đồ thị hàm số bên phải và bên trái trục Oy trùng nhau.
Luyện tập2
Giải câu hỏi Luyện tập 2 trang 5
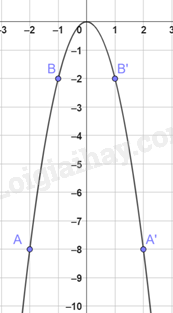
Vẽ đồ thị y = -2x2.

Cách vẽ đồ thị \(y = a{x^2}\left( {a \ne 0} \right)\) như sau:
- Vẽ hệ trục toạ độ Oxy.
- Lập bảng một số giá trị tương ứng của x và y. Đánh dấu các điểm tương ứng trên mặt phẳng toạ độ. Ta thường lấy điểm O và những điểm có hoành độ đối nhau.
- Vẽ đường thẳng parabol đi qua các điểm vừa đánh dấu.

Bảng một số giá trị tương ứng x và y:

Trên mặt phẳng toạ độ, đánh dấu các điểm A(-2;-8), B(-1;-2), O(0;0), B’(1;-2), A’(2; -8).
Đồ thị hàm số y = -2x2 là đường parabol đi qua năm điểm A, B, O, B’, A’.
Vận dụng2
Gợi ý giải câu hỏi Vận dụng 2 trang 5
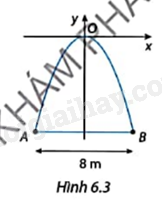
Một cổng chào được thiết kế theo hình parabol là một phần của đồ thị hàm số \(y = - \frac{{{x^2}}}{2}\). Khoảng cách giữa hai chân cổng là AB = 8 m (Hình 6.3).
a) Tìm hoành độ của hai điểm A, B.
b) Tìm chiều cao của cổng.

Từ khoảng cách AB = 8 suy ra hoành độ x.
Chiều cao của cổng chính là tung độ y.
Thay x vào \(y = - \frac{{{x^2}}}{2}\) để tìm y.

a) Khoảng cách AB = 8 nên OA = OB = \(\frac{{AB}}{2} = \frac{8}{2} = 4\).
Vậy hoành độ điểm B là 4, hoành độ điểm A là – 4
b) Thay x = 4 vào \(y = - \frac{{{x^2}}}{2}\) ta có: \( - \frac{{{4^2}}}{2} = - 8\).
Vậy chiều cao của cổng là 8 m.
