Giải mục 3 trang 119, 120, 121 Toán 9 Cùng khám phá tập 1: Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây...

Hoạt động4

Trả lời câu hỏi Hoạt động 4 trang 119

Quay lại hoạt động gấp hình tròn trong Hoạt động 1.

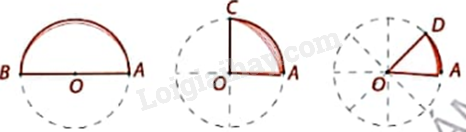
Hãy xác định các số đo cung và tỉ số trong các ô ? của bảng dưới đây. Em có nhận xét gì?

+ Số đo các cung AB, AC, AD lần lượt có số đo là ${180^o}$, ${90^o}$, ${45^o}$.

+ Tỉ số của số đo cung và ${360^o}$ bằng thương giữa số đo cung tương ứng và ${360^o}$.

+ Nhận xét: Tỉ số của số đo cung và ${360^o}$ bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.

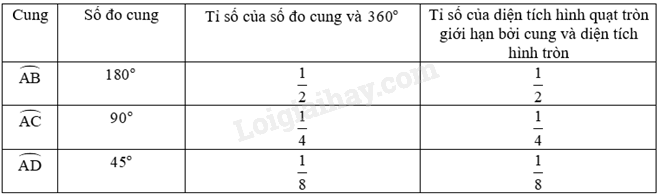
Nhận xét: Tỉ số của số đo cung và ${360^o}$ bằng tỉ số của diện tích hình quạt tròn giới hạn bởi cung và diện tích hình tròn.

Luyện tập3

Trả lời câu hỏi Luyện tập 3 trang 120

Tính diện tích của hình quạt tròn bán kính 3cm ứng với cung ${210^o}$.

Công thức tính diện tích hình quạt tròn bán kính R ứng với cung ${n^o}$: ${S_q} = \frac{{\pi {R^2}n}}{{360}}$.

Diện tích của hình quạt tròn bán kính 3cm ứng với cung ${210^o}$ là:

${S_q} = \frac{{\pi {{.3}^2}.210}}{{360}} = \frac{{21\pi }}{4}\left( {c{m^2}} \right)$.

Luyện tập4

Trả lời câu hỏi Luyện tập 4 trang 120

Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm.

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; R) và (O; r) (với $r < R$): ${S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)$.

Diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm là:

${S_{vk}} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {c{m^2}} \right)$.

Vận dụng

Trả lời câu hỏi Vận dụng trang 121

Trong Hình 5.54, chiếc quạt có dạng một hình quạt tròn tâm O cung AB, bán kính $OA = OB = 20cm$. Giấy được dán trong phần giới hạn bởi cung AB, cung CD, đoạn thẳng AC và BD với $OC = OD = 10cm$. Biết khi mở rộng tối đa, hai nan quạt ngoài cùng tạo thành một góc $\widehat {AOB} = {140^o}$. Tính chu vi và diện tích mảnh giấy để dán một mặt quạt (diện tích mép không đáng kể).

Công thức tính độ dài cung ${n^o}$ của đường tròn bán kính R: $l = \frac{{\pi Rn}}{{180}}$.

Công thức tính diện tích hình quạt tròn bán kính R ứng với cung ${n^o}$: ${S_q} = \frac{{\pi {R^2}n}}{{360}}$.

Ta có: $BD = AC = OB - OD = 20 - 10 = 10cm$.

Diện tích hình quạt tâm O, cung AB là:

${S_{AOB}} = \frac{{\pi {{.20}^2}.140}}{{360}} = \frac{{1400}}{9}\pi \left( {c{m^2}} \right)$.

Diện tích hình quạt tâm O, cung CD là:

${S_{COD}} = \frac{{\pi {{.10}^2}.140}}{{360}} = \frac{{350}}{9}\pi \left( {c{m^2}} \right)$.

Diện tích mảnh giấy để dán một mặt quạt là:

$S = {S_{AOB}} - {S_{COD}} = \frac{{1400}}{9}\pi - \frac{{350}}{9}\pi = \frac{{350}}{3}\pi \left( {c{m^2}} \right)$.

Độ dài cung AB là:

${l_{AB}} = \frac{{\pi .20.140}}{{180}} = \frac{{140}}{9}\pi \left( {cm} \right)$.

Độ dài cung CD là:

${l_{CD}} = \frac{{\pi .10.140}}{{180}} = \frac{{70}}{9}\pi \left( {cm} \right)$.

Chu vi mảnh giấy để dán một mặt quạt là:

$AC + BD + {l_{AB}} + {l_{CD}} = 10 + 10 + \frac{{140\pi }}{9} + \frac{{70\pi }}{9} = 20 + \frac{{70\pi }}{3}\left( {cm} \right)$