
Trên một dãy phố có ba quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa.
a) Mô tả không gian mẫu của phép thử.
b) Tính xác suất của các biến cố sau:
E: “Hai bạn cùng vào một quán”;
F: “Cả hai bạn không chọn quán C”;
G: “Có ít nhất một bạn chọn quán B”.

a) Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Ta có thể tìm số phần tử của không gian mẫu bằng cách lập bảng.
b) Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Advertisements (Quảng cáo)
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).

a) Ta liệt kê tất cả các kết quả có thể của phép thử bằng cách lập bảng:
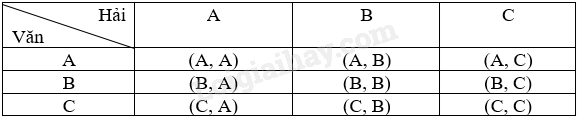
Không gian mẫu của phép thử là: \(\Omega = \){(A, A), (B, A), (C, A), (A, B), (B, B), (C, B), (A, C), (B, C), (C, C)}. Vậy không gian mẫu có 9 phần tử.
b) Vì hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa nên các kết quả có thể của phép thử là đồng khả năng.
Có 3 kết quả thuận lợi của biến cố E là: (A, A), (B, B), (C, C). Do đó, \(P\left( E \right) = \frac{3}{9} = \frac{1}{3}\).
Có 4 kết quả thuận lợi của biến cố F là: (A, A), (B, B), (A, B), (B, A). Do đó, \(P\left( F \right) = \frac{4}{9}\).
Có 5 kết quả thuận lợi của biến cố G là: (C, B), (B, B), (A, B), (B, A), (B, C). Do đó, \(P\left( G \right) = \frac{5}{9}\).
