
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
E: “Có đúng một con xúc xắc xuất hiện mặt 6 chấm”;
F: “Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm”;
G: “Tích của hai chấm xuất hiện trên hai con xúc xắc nhỏ hơn hoặc bằng 6”.

Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Advertisements (Quảng cáo)
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).

Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là số chấm xuất hiện trên hai con xúc xắc I và II.
Ta có bảng miêu tả không gian mẫu là:
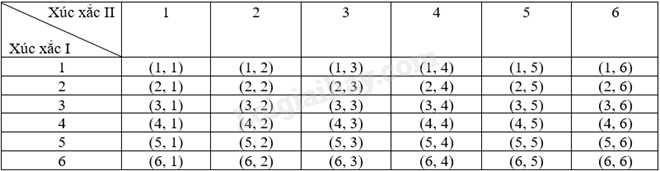
Do đó, số phần tử của không gian mẫu \(\Omega \) là 36.
Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy là đồng khả năng.
Có 10 kết quả thuận lợi của biến cố E là: (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5). Do đó, \(P\left( E \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).
Có 11 kết quả thuận lợi của biến cố F là: (1, 6), (2, 6), (3, 6), (4, 6), (5, 6), (6, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5). Do đó, \(P\left( F \right) = \frac{{11}}{{36}}\).
Có 14 kết quả thuận lợi của biến cố G là: (1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (1, 4), (1, 5), (1, 6). Do đó, \(P\left( G \right) = \frac{{14}}{{36}} = \frac{7}{{18}}\).
