Câu hỏi/bài tập:

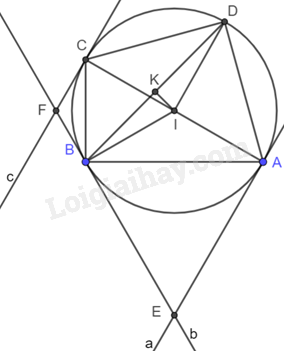
Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C).
b) Gọi I và K lần lượt là trung điểm của các đường chéo AC và BD của tứ giác. Chứng minh rằng \(IK \bot BD\).
c) Kí hiệu các tiếp tuyến của đường tròn (C) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang.
d) Chứng minh rằng \(EF = AE + CF\).

a) Chứng minh tam giác ABC vuông tại B, tam giác ADC vuông tại D nên đường tròn đường kính AC đi qua bốn điểm A, B, C, D.
b) + Chứng minh I là tâm đường tròn đường kính AC.
+ Chứng minh tam giác IBD cân tại I nên IK là đường trung tuyến đồng thời là đường cao.
c) Chứng minh \(FC \bot AC\), \(AE \bot AC\) nên FC//AE. Do đó, tứ giác AEFC là hình thang.
d) Chứng minh \(FC = FB\), \(EA = EB\) nên \(EF = AE + CF\).
Advertisements (Quảng cáo)

a) \(\Delta \)ABC có \(\widehat {ABC} = {90^o}\) nên \(\Delta \)ABC vuông tại B. Do đó, B thuộc đường tròn đường kính AC.
\(\Delta \)ADC có \(\widehat {ADC} = {90^o}\) nên \(\Delta \)ADC vuông tại D. Do đó, D thuộc đường tròn đường kính AC.
Vậy đường tròn đường kính AC đi qua bốn điểm A, B, C, D.
b) Vì I là trung điểm của AC nên đường tròn tâm I, đường kính AC đi qua bốn điểm A, B, C, D.
Do đó, \(IB = ID\) nên \(\Delta \)IBD cân tại I. Suy ra, IK là đường trung tuyến đồng thời là đường cao.
Suy ra, \(IK \bot BD\).
c) Vì FC là tiếp tuyến của (I, IC) nên \(FC \bot AC\). Vì AE là tiếp tuyến của (I, IC) nên \(AE \bot AC\).
Vì \(FC \bot AC\), \(AE \bot AC\) nên FC//AE. Do đó, tứ giác AEFC là hình thang.
d) Vì FB và FC là hai tiếp tuyến của (I, IC) nên \(FC = FB\).
Vì EA và EB là hai tiếp tuyến của (I, IC) nên \(EA = EB\).
Do đó, \(AE + CF = EB + FB = EF\)
