Câu hỏi/bài tập:

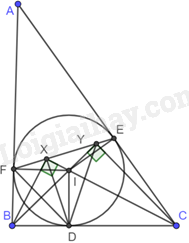
Cho tam giác ABC \(\left( {AB < AC} \right)\) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:
a) DBXF, DCYE là các tứ giác nội tiếp.
b) Bốn điểm X, Y, E, F thẳng hàng.

a) Chứng minh tam giác IFB vuông tại F, tam giác BID vuông tại D, tam giác BXI vuông tại X nên 5 điểm I, B, D, F, X thuộc đường tròn đường kính BI. Do đó, tứ giác DBFX nội tiếp.
Chứng minh tương tự ta có tứ giác DCEY là tứ giác nội tiếp.
b) Chứng minh tứ giác XYCB nội tiếp nên \(\widehat {YXC} = \widehat {YBC}\)
+ Chứng minh \(\widehat {FXB} = \widehat {FDB}\).
+ Chứng minh BI là trung trực của DF. Suy ra, \(BI \bot FD\). Do đó, \(\widehat {YBC} + \widehat {FDB} = {90^o}\)
+ Chứng minh \(\widehat {FXB} + \widehat {YXC} = {90^o}\)
+ Chứng minh \(\widehat {FXY} = \widehat {FXB} + \widehat {YXC} + \widehat {BXC} = {180^o}\) nên 3 điểm F, X, Y thẳng hàng.
+ Chứng minh tương tự ta có: 3 điểm X, Y, E thẳng hàng.

Advertisements (Quảng cáo)
a) Vì ID, IE, IF là tiếp tuyến của đường tròn (I) nên \(IF \bot BF,ID \bot BC,IE \bot AC\)
Do đó, \(\widehat {IFB} = \widehat {IDB} = \widehat {IDC} = \widehat {IEC} = {90^o}\)
Suy ra, \(\Delta \)IFB vuông tại F, \(\Delta \)BID vuông tại D nên 4 điểm I, B, D, F thuộc đường tròn đường kính BI.
\(\Delta \)BXI vuông tại X nên X thuộc đường tròn đường kính BI.
Do đó, 5 điểm I, B, D, F, X thuộc đường tròn đường kính BI. Do đó, tứ giác DBFX nội tiếp.
Chứng minh tương tự ta có: tứ giác DCEY là tứ giác nội tiếp.
b) Vì \(\Delta \)BXC vuông tại X, \(\Delta \)BYC vuông tại Y nên 4 điểm B, X, Y, C thuộc đường tròn đường kính BC. Do đó, \(\widehat {YXC} = \widehat {YBC}\) (1) (góc nội tiếp cùng chắn cung YC).
Xét đường tròn đường kính BI có: \(\widehat {FXB} = \widehat {FDB}\) (2) (góc nội tiếp cùng chắn cung BF).
Vì BF và BD là tiếp tuyến của đường tròn (I) nên \(BF = BD\) nên B thuộc đường trung trực của DF.
Lại có: \(IF = ID\) (bán kính đường tròn (I)) nên I thuộc đường trung trực của DF.
Do đó, BI là trung trực của DF. Suy ra, \(BI \bot FD\). Do đó, \(\widehat {YBC} + \widehat {FDB} = {90^o}\) (3).
Từ (1), (2) và (3) ta có: \(\widehat {FXB} + \widehat {YXC} = {90^o}\)
Do đó, \(\widehat {FXY} = \widehat {FXB} + \widehat {YXC} + \widehat {BXC} = {90^o} + {90^o} = {180^o}\). Do đó, 3 điểm F, X, Y thẳng hàng.
Chứng minh tương tự ta có: 3 điểm X, Y, E thẳng hàng.
Vậy X, Y, E, F thẳng hàng.
