Câu hỏi/bài tập:

Kí hiệu \(\left( {{d_1}} \right)\) là đường thẳng \(x + 2y = 4,\left( {{d_2}} \right)\) là đường thẳng \(x - y = 1\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - y = 1\end{array} \right.\) để tìm tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).

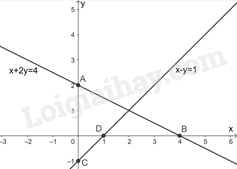
a) Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right),B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {0; - 1} \right),D\left( {1;0} \right)\).
Biểu diễn các điểm A, B, C, D trên cùng một mặt phẳng tọa độ Oxy.
b) Giải hệ phương trình bằng phương pháp cộng đại số: Để giải một hệ hai phương trình bậc nhất hai ẩn có hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau, ta có thể làm như sau:
Advertisements (Quảng cáo)
Bước 1. Cộng hay trừ từng vế của hai phương trình trong hệ được phương trình chỉ còn chứa một ẩn.
Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.
+ Trường hợp hệ phương trình đã cho không có hai hệ số của cùng một ẩn bằng nhau hoặc đối nhau, ta có thể đưa về trường hợp đã xét bằng cách nhân hai vế của mỗi phương trình với một số thích hợp (khác 0).

a) Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right),B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {0; - 1} \right),D\left( {1;0} \right)\).
b) Trừ từng vế hai phương trình ta được \(\left( {x + 2y} \right) - \left( {x - y} \right) = 4 - 1\), hay \(3y = 3\), suy ra \(y = 1\).
Thế \(y = 1\) vào phương trình thứ hai của hệ đã cho ta có: \(x - 1 = 1\) nên \(x = 2\).
Do đó, tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là (2; 1).
