
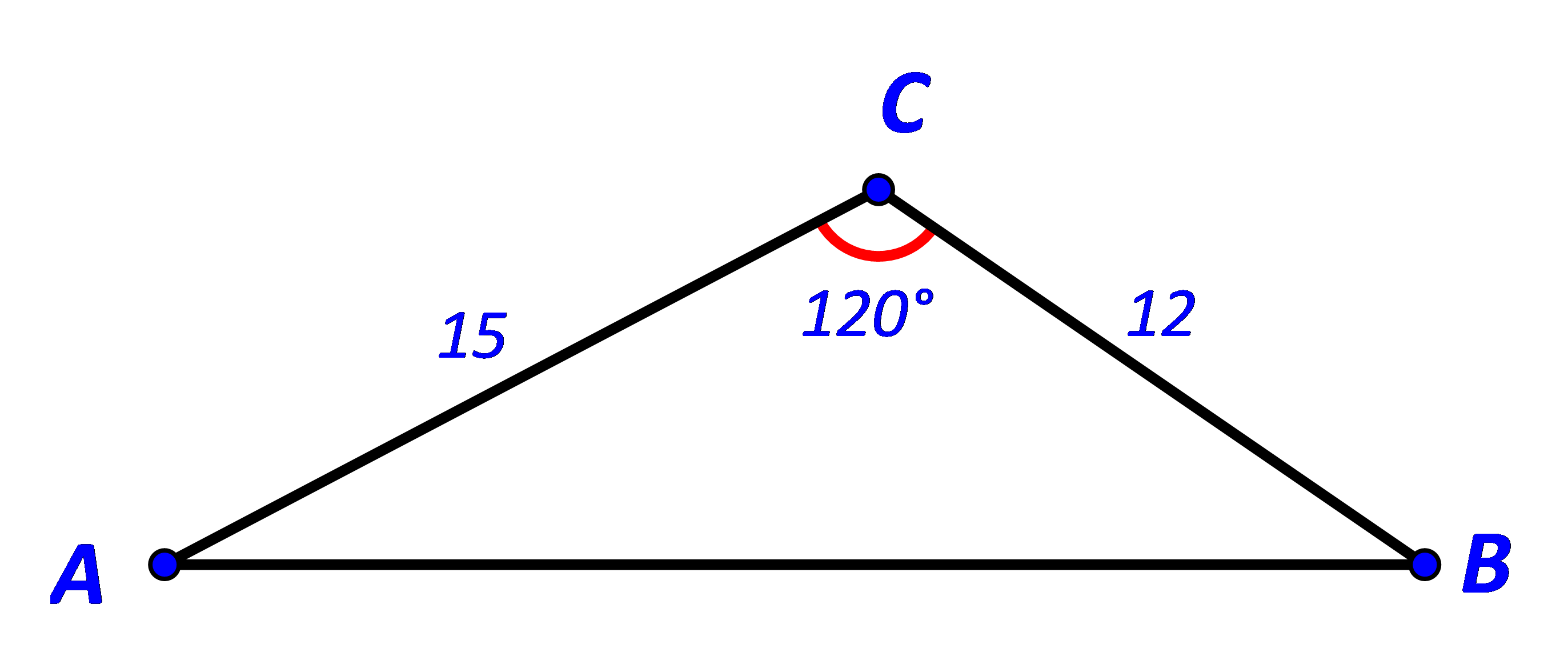
Cho tam giác ABC có \(BC = 12,CA = 15,\widehat C = {120^o}.\) Tính:
a) Độ dài cạnh AB.
b) Số đo các góc A, B.
c) Diện tích tam giác ABC.

a) Áp dụng định lí cosin trong tam giác ABC (tại đỉnh C).
b)
Bước 1: Tính sin A, bằng cách áp dụng định lí sin trong tam giác ABC: \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\).
Bước 2: Tính góc A, từ đó suy ra góc B.
c) Tính diện tích tam giác ABC bằng công thức \(S = \frac{1}{2}ab.\sin C\)
Advertisements (Quảng cáo)

a) Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}\)
b) Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44\)
\( \Rightarrow \widehat A \approx {26^o}\) hoặc \(\widehat A \approx {154^o}\) (Loại)
Khi đó: \(\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}\)
c)
Diện tích tam giác ABC là: \(S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3 \)
