Hoạt động 2
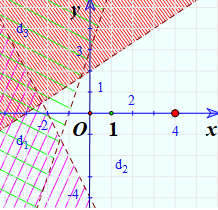
Cho hệ bất phương trình sau: \(\left\{ \begin{array}{l}x - 2y \ge - 2\\7x - 4y \le 16\\2x + y \ge - 4\end{array} \right.\)
a) Trong cùng mặt phẳng toạ độ Oxy, biểu diễn miền nghiệm của mỗi bất phương trình
trong hệ bất phương trình bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.
b) Tìm miền nghiệm của hệ bất phương trình đã cho.

a) Biểu diễn miền nghiệm của 3 bất phương trình trên cùng một mặt phẳng tọa độ.
b) Miền nghiệm của hệ là miền nghiệm chung của 3 bất phương trình.

a) Trong cùng mặt phẳng toạ độ Oxy, vẽ ba đường thẳng:
\({d_1}:x - 2y = - 2\);
\({d_2}:7x - 4y = 16\)
\({d_3}:2x + y = - 4\)
Thay tọa độ điểm O vào \(x - 2y\) ta được:
\(0 - 2.0 = 0 \ge - 2\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(7x - 4y\) ta được:
\(7.0 - 4.0 = 0 \le 16\)
=> Điểm O thuộc miền nghiệm
=> Gạch phần không chứa điểm O.
Thay tọa độ điểm O vào \(2x + y\) ta được:
\(2.0 + 0 = 0 \ge - 4\)
=> Điểm O thuộc miền nghiệm
Advertisements (Quảng cáo)
=> Gạch phần không chứa điểm O.
b)
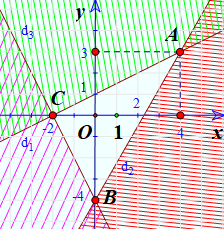
Miền nghiệm của hệ là phần không bị gạch bỏ chung của cả 3 miền nghiệm trên.
Chú ý
Ở câu a, có thể thay điểm O bằng các điểm khác.
Luyện tập - vận dụng 2
Biểu diễn miền nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x - y > - 3\\ - 2x + 3y < 6\\2x + y > - 4\end{array} \right.\)

Bước 1: Vẽ các đường thẳng.
Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Bước 3: Phần không bị gạch là miền nghiệm.

Vẽ đường thẳng \(3x - y = - 3\) (nét đứt)
Thay tọa độ O vào \(3x - y > - 3\) ta được \(3.0 - 0 > - 3\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \( - 2x + 3y = 6\) (nét đứt)
Thay tọa độ O vào \( - 2x + 3y < 6\) ta được \( - 2.0 + 3.0 < 6\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \(2x + y = - 4\)(nét đứt)
Thay tọa độ O vào \(2x + y > - 4\) ta được \(2.0 + 0 > - 4\) (Đúng)
Gạch đi phần không chứa O
Miền nghiệm của hệ là phần không bị gạch chéo: