
Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh, 1 thẻ đỏ. Các tấm thẻ có kích thước có khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ
a) Sử dụng sơ đồ hình cây, hãy liệt kê tất cả các kết quả có thể xảy ra
b) Tính xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”

Advertisements (Quảng cáo)
a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
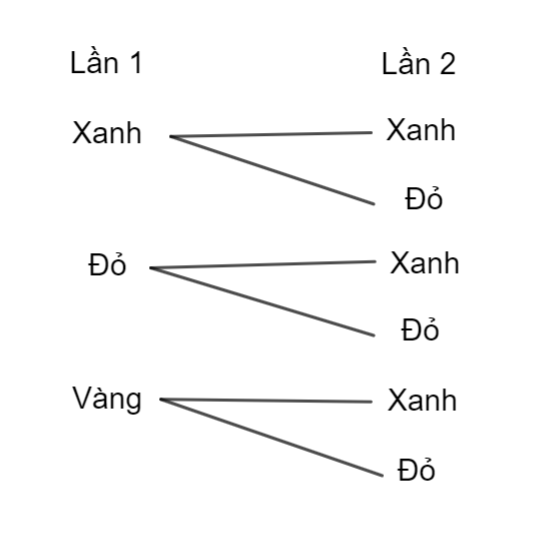
b)
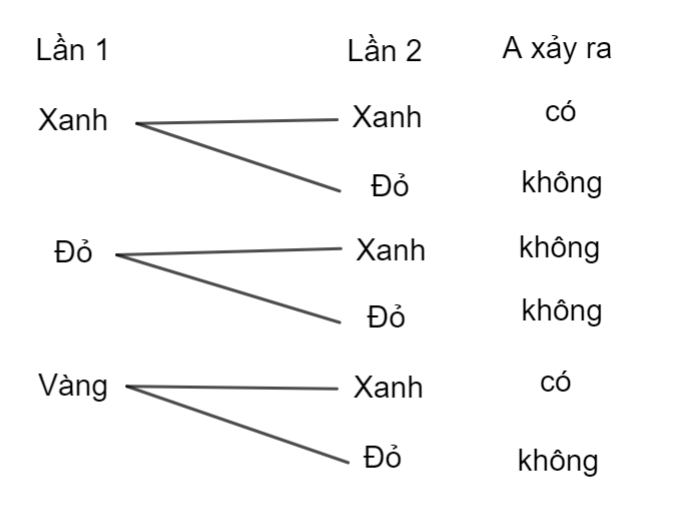
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\)
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\)
