Lời giải bài 2.6 trang 30 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài 4: Hệ bất phương trình bậc nhất hai ẩn
![]()
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 250 nghìn đồng; 1kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.
a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.
c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.
![]()
a) Vì gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn nên 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1
Nếu mua x kilôgam thịt bò và y kilôgam thịt lợn thì chứa số đơn vị protein là: 800x + 600y (đơn vị)
Do số đơn vị protein cần ít nhất là 900 đơn vị nên ta có: 800x + 600y ≥ 900 hay 8x + 6y ≥ 9
Nếu mua x kilôgam thịt bò và y kilôgam thịt lợn thì chứa số đơn vị lipit là: 200x + 400y (đơn vị)
Do số đơn vị lipit cần ít nhất là 400 đơn vị nên ta có: 200x + 400y ≥ 400 hay x + 2y ≥ 2
Khi đó ta có hệ bất phương trình:
Advertisements (Quảng cáo)
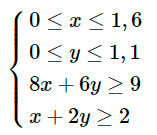
Miền nghiệm của hệ bất phương trình trên là tứ giác ABCD với tọa độ các đỉnh A(0;1), B(1,6;0,2) và C(1,6;1,1), D(0;1,1)

b) Vì số tiền mỗi kg thịt bò và thịt lợn lần lượt là 250 nghìn đồng và 160 nghìn đồng nên ta có
(nghìn đồng)
Vậy F(x;y) = 250x + 160y
c) Tính giá trị của biểu thức F tại các đỉnh của tam giác này:
F(1;0) = 250.1 + 160.0 = 250;
F(1,6;0,2) = 250.1,6 + 160.0,2 = 432;
F(1,6;1,1) = 250.1,6 + 160.1,1 = 576;
F(0;1,1) = 250.0 + 160.1,1 = 176;
Suy ra giá trị nhỏ nhất cần tìm là F(0;1,1) = 176.
Vậy để chi phí là ít nhất thì gia đình cần mua 0 kilôgam thịt bò và 1,1 kilôgam thịt lợn.
