Giải bài 2.5 trang 30 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài 4: Hệ bất phương trình bậc nhất hai ẩn
![]()
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:
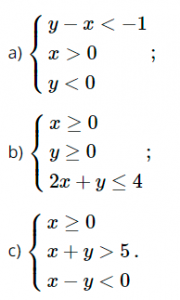
![]()
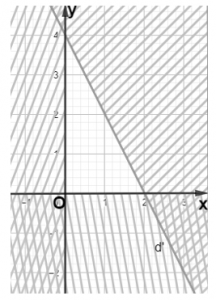
a) Xác định miền nghiệm D1 của bất phương trình y – x < - 1 và gạch bỏ miền nghiệm còn lại.
- Vẽ đường thẳng d: - x + y + 1 = 0.
- Vì 0 - 0 = 0 > -1 nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình y – x < -1.
Do đó miền nghiệm D1 của bất phương trình y – x < - 1 là nửa mặt phẳng bờ d không chứa gốc tọa độ và không chứa biên.
Miền nghiệm D2 của bất phương trình x > 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0) và không chứa biên.
Miền nghiệm D3 của bất phương trình y < 0 là nửa mặt phẳng bờ Ox chứa điểm (0;-1) và không chứa biên.
Vậy miền không bị gạch (không kể biên) chính là giao các miền nghiệm của các bất phương trình trong hệ.
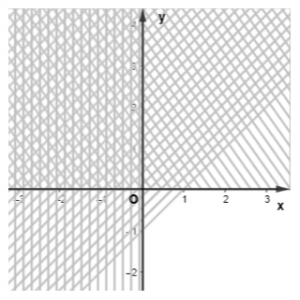
b)
Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).
Xác định miền nghiệm D3 của bất phương trình 2x + y ≤ 4 và gạch bỏ miền nghiệm còn lại.
- Vẽ đường thẳng d’: 2x + y – 4 = 0.
Advertisements (Quảng cáo)
- Vì 2.0 + 0 = 0 < 4 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình 2x + y ≤ 4.
Do đó miền nghiệm D3 của bất phương trình 2x + y ≤ 4 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.
Khi đó miền không bị gạch chính là giao các miền nghiệm của các bất phương trình trong hệ. Vậy miền nghiệm của hệ miền không bị gạch trong hình dưới đây:
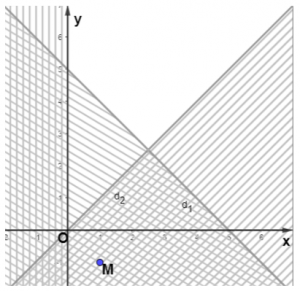
c)
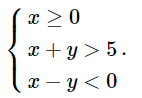
Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Miền nghiệm D2 của bất phương trình x + y > 5 và gạch bỏ miền nghiệm còn lại.
- Vẽ đường thẳng d1: x + y – 5 = 0.
- Vì 0 + 0 = 0 < 5 nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình x + y > 5.
Do đó miền nghiệm D2 của bất phương trình x + y > 5 là nửa mặt phẳng bờ d1 không chứa gốc tọa độ và không chứa đường thẳng d1.
Xác định miền nghiệm D3 của bất phương trình x - y < 0 và gạch bỏ miền nghiệm còn lại.
- Vẽ đường thẳng d2: x – y = 0.
- Vì 1 – (-1) = 2 > 0 nên tọa độ điểm M(1;-1) không thỏa mãn bất phương trình x – y < 0.
Do đó miền nghiệm D3 của bất phương trình x – y < 0 là nửa mặt phẳng bờ d2 không chứa điểm M(1;-1).
Khi đó miền không bị gạch và không chứa biên chính là giao các miền nghiệm của các bất phương trình trong hệ. Vậy miền nghiệm của hệ miền không bị gạch trong hình dưới dây: