Advertisements (Quảng cáo)
Bài 1.45 trang 14 Sách bài tập (SBT) Vật lí 11 nâng cao
Một điện tích điểm \(q = + 10\mu C\) chuyển động từ đỉnh B đến đỉnh C của tam giác đều ABC. Tam giác ABC nằm trong điện trường đều có cường độ 5000 V/m. Đường sức của điện trường này song song với cạnh BC và có chiều từ C đến B. Cạnh của tam giác bằng 10 cm. Tính công của lực điện khi điện tích q chuyển động trong hai trường hợp sau :
a, q chuyển động theo đoạn thẳng BC.
b, q chuyển động theo đoạn gấp khúc BAC. Tính công trên các đoạn BA, AC và coi công trên đoạn đường BC bằng tổng các công trên hai đoạn đường trên.
Lực tác dụng lên điện tích q trong hai trường hợp được vẽ trên Hình 1.8G.
Advertisements (Quảng cáo)
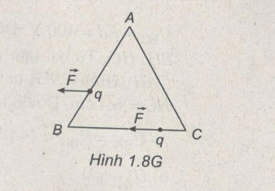
a, \({A_{BC}} = – Fs = – qE.BC = – {5.10^{ – 3}}J.\)
b, \({A_{BA}} = – Fs\cos {60^o} \) \(= – qE\cos {60^o}.BA = – 2,{5.10^{ – 3}}J\)
\({A_{AC}} = – Fs\cos {60^o} \) \(= – qE\cos {60^o}.AC = – 2,{5.10^{ – 3}}J.\)
\({A_{BC}} = {A_{BA}} + {A_{AC}} = – 5,{0.10^{ – 3}}J.\) Kết quả này là tất nhiên vì công của lực điện không phụ thuộc vào dạng của đoạn đường dịch chuyển của điện tích .