Advertisements (Quảng cáo)
Bài 7.58 trang 93 Sách bài tập (SBT) Vật lí 11 nâng cao
Một ống nhòm Ga-li-lê cấu tạo bởi vật kính có tiêu cự \({f_1} = 25cm\) và thị kính có độ tụ là \( – 10dp\).
a) Hãy thông qua việc dựng ảnh để chứng minh rằng, nếu tiêu điểm ảnh \({F_1}\) của vật kính nằm ngoài khoảng \({O_2}{F_2}\) của thị kính (\({F_2}\) là tiêu điểm vật của thị kính) thì ảnh cuối cùng của một vật đặt ở xa vô cực sẽ là ảnh ảo và cùng chiều với vật.
b) Một mắt thường đặt sát thị kính, ngắm chừng ở vô cực để quan sát ảnh cuối cùng qua kính. Tính chiều dài của kính và số bội giác của nó.
c) Dùng kính ở câu b quan sát một tháp cao 50 m, xa 2 km sẽ thấy ảnh của nó dưới góc trông là bao nhiêu ?
a) Hình vẽ : Học sinh tự vẽ.
b) Sơ đồ tạo ảnh :
\(AB\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{{d_1} = \infty }} {O_1}\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{d{‘_1}}} \mathop {{A_1}{B_1}}\limits_{\left( {F{‘_1}} \right)} \mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{{d_2}}} {O_2}\) \(\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{d{‘_2} = \infty }} {A_2}{B_2}\) (ở vô cực)
Vì ngắm chừng ở vô cực nên \({A_2}{B_2}\) ở vô cực \( \Rightarrow {A_1}{B_1} \equiv {F_2} \Rightarrow F{‘_1} \equiv F{‘_2}\)
Advertisements (Quảng cáo)
\(\eqalign{
& {O_1}{O_2} = {O_1}F{‘_1} – {O_2}F{‘_1} \cr&\;\;\;\;\;\;\;\;\;\,= {O_1}F{‘_1} – {O_2}{F_2} = {f_1} – \left| {{f_2}} \right| \cr
& {f_2} = – {1 \over {10}}m = – 10cm \cr
& {O_1}{O_2} = 25cm – 10cm = 15cm \cr
& G = {\alpha \over {{\alpha _0}}} \cr
& {\alpha _0} \approx {{{A_1}{B_1}} \over {{f_1}}} \cr
& \alpha = \widehat {{A_1}{O_2}{B_1}} \cr} \)
(Xem Hình 7.2G)
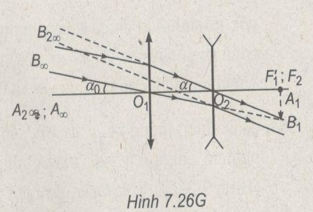
\(\eqalign{
& \alpha \approx \tan \alpha = {{{A_1}{B_1}} \over {{O_2}{F_2}}} = {{{A_1}{B_1}} \over {\left| {{f_2}} \right|}} \cr
& G = {{{A_1}{B_1}} \over {\left| {{f_2}} \right|}}.{{{f_1}} \over {{A_1}{B_1}}} = {{{f_1}} \over {\left| {{f_2}} \right|}} = {{25} \over {10}} \cr&\;\;\;\;= 2,5 \cr} \)
c) Với \(AB = 50m;A{O_1} = 2km = 2000m\) thì ta có:
\({\alpha _0} \approx \tan {\alpha _0} = {{AB} \over {A{O_1}}} = {{50} \over {2000}} \) \(= {25.10^{ – 3}}rad\)
\(\alpha = G.{\alpha _0} = 2,{5.25.10^{ – 3}}rad \) \(= 6,{25.10^{ – 2}}rad\)