
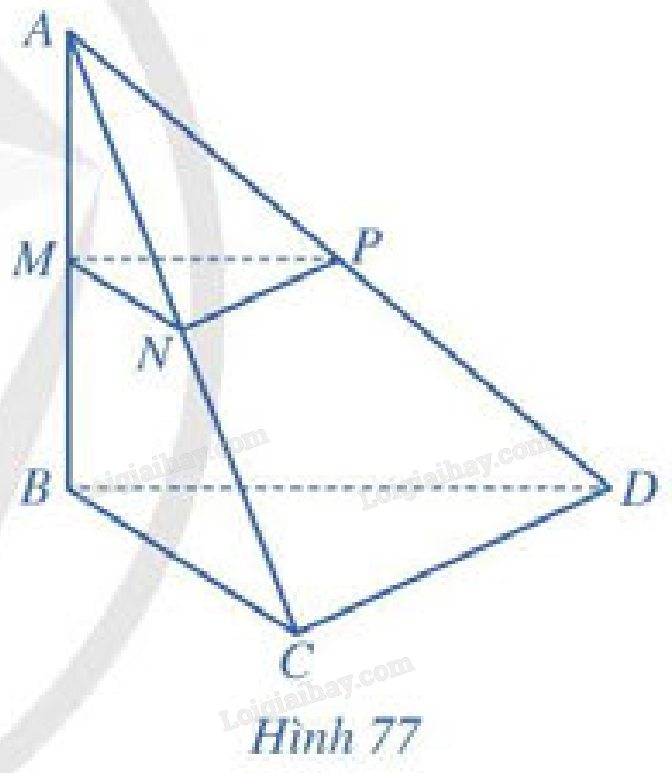
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).
a) Tính khoảng cách từ điểm \(C\) đến đường thẳng \(AB\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\).
c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(C{\rm{D}}\).

‒ Cách tính khoảng cách từ một điểm đến một đường thẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên đường thẳng.
‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Advertisements (Quảng cáo)
‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

a) \(\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC \Rightarrow d\left( {C,AB} \right) = BC = b\).
b)
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC\\\widehat {ABD} = {90^ \circ } \Rightarrow AB \bot BD\end{array} \right\} \Rightarrow AB \bot \left( {BC{\rm{D}}} \right)\\\left. \begin{array}{l} \Rightarrow AB \bot C{\rm{D}}\\\widehat {BC{\rm{D}}} = {90^ \circ } \Rightarrow BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABC} \right)\\ \Rightarrow d\left( {D,\left( {ABC} \right)} \right) = C{\rm{D}} = \sqrt {B{{\rm{D}}^2} - B{C^2}} = \sqrt {{c^2} - {b^2}} \end{array}\)
c) \(AB \bot BC,C{\rm{D}} \bot BC \Rightarrow d\left( {AB,C{\rm{D}}} \right) = BC = b\).
