
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(O\), \(SO \bot \left( {ABCD} \right)\), tam giác \(SAC\) là tam giác đều.
a) Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\).
b) Chứng minh rằng \(AC \bot \left( {SBD} \right)\). Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).
c) Gọi \(M\) là trung điểm của cạnh \(AB\). Tính số đo của góc nhị diện \(\left[ {M,SO,D} \right]\).

‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
‒ Cách tính chứng minh đường thẳng vuông góc với mặt phẳng: Chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

Advertisements (Quảng cáo)
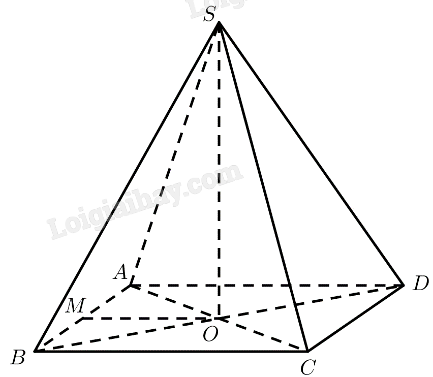
a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)
\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)
b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)
\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)
Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)
\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)
\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)
\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).
