Bài 2 trang 99 Toán 11 tập 2 - Cánh Diều: Chứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một...

Chứng minh định lí sau: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

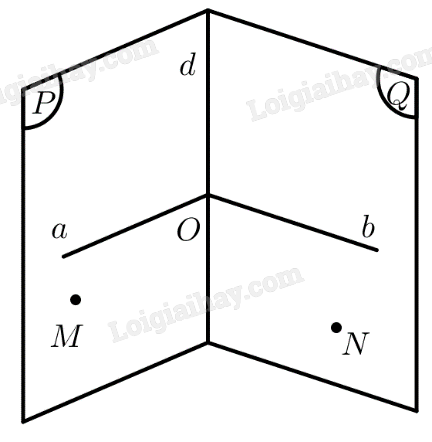
Cho hai mặt phẳng $\left( P \right),\left( Q \right)$ vuông góc với nhau. Ta cần chứng minh tồn tại một đường thẳng $a \subset \left( P \right)$ sao cho $a \bot \left( Q \right)$.

Gọi $d = \left( P \right) \cap \left( Q \right)$. Lấy $M \in \left( P \right),N \in \left( Q \right)$ sao cho $M,N \notin d$.

Gọi góc $\widehat {aOb}$ là góc phẳng nhị diện của góc nhị diện $\left[ {M,d,N} \right]$.

Vì $\left( P \right) \bot \left( Q \right)$ nên góc nhị diện đó là góc nhị diện vuông. Vậy $\widehat {aOb} = {90^ \circ } \Rightarrow a \bot b$.

Mà $a \bot d$

$\Rightarrow a \bot \left( Q \right)$