
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.

Chứng minh giao điểm của ba đường thẳng nằm trên cùng một mặt phẳng, khi đó a, b, c cùng thuộc một mặt phẳng (trái với giả thiết) => giao điểm của ba đường thẳng phải trùng nhau.

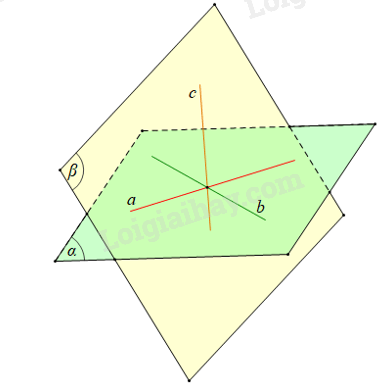
Giả sử a ∩ b = {I} và α = mp(a, b);
a ∩ c = {J} và β = mp(a, c);
Advertisements (Quảng cáo)
b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.
Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.
α ∩ γ = b và đường thẳng b chính là đường thẳng IK.
β ∩ γ = c và đường thẳng c chính là đường thẳng JK.
Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)
Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.
Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.
